Institute of Oceanology, Chinese Academy of Sciences
Article Information
- LIU Kun(刘昆), XU Zhenhua(徐振华), YIN Baoshu(尹宝树)
- Three-dimensional numerical simulation of internal tides that radiated from the Luzon Strait into the Western Pacific
- Chinese Journal of Oceanology and Limnology, 35(6): 1275-1286
- http://dx.doi.org/10.1007/s00343-017-5376-2
Article History
- Received Jan. 8, 2016
- accepted in principle Mar. 15, 2016
- accepted for publication Sep. 19, 2016
2 Key Laboratory of Ocean Circulation and Waves(KLOCAW), Chinese Academy of Sciences, Qingdao 266071, China;
3 Laboratory for Ocean and Climate Dynamics, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China;
4 University of Chinese Academy of Sciences, Beijing 100049, China
When barotropic tidal currents flow over a rough seafloor, internal tides (ITs) are generated and then propagate obliquely within the stratified ocean (Garrett, 2003). ITs play a significant role in deep-sea mixing, and they provide half the energy required to sustain the large-scale thermocline circulation on the global scale (Egbert and Ray, 2000). ITs are concentrated mainly in areas with sharp topography, and thus they are not as vast as astronomical tides. Globally, about 75% of M2 ITs are generated at around 20 sites with abrupt topography (Simmons et al., 2004). The Luzon Strait (LS) is the main water channel connecting the Western Pacific (WP) and the South China Sea (SCS), where considerable tidal energy is gathered within a relatively short distance of several hundreds of kilometers. Featuring the unique structure of a meridional double-ridge system and responsible for driving zonal tidal currents, the LS is one of the most active areas in the world for the generation of ITs (Xu et al., 2014). Peak baroclinic velocities of up to 2 m/s and vertical isopycnal displacements exceeding 300 m have been observed (Alford et al., 2011). Large-amplitude internal solitary waves originating from nonlinear steepening of ITs have been observed and examined extensively in recent years (Liu et al., 1998, 2013; Xu et al., 2010, 2012).
The majority of studies of ITs generated at the LS have focused primarily on the near field around the generation area and the north SCS. The variation of ITs generated at the LS (Jan et al., 2008; Xu et al., 2011, 2013; Buijsman et al., 2013) and tidal beam propagation in the north SCS (Miao et al., 2011; Ma et al., 2013) have been discussed, but the extent to which ITs propagate into the Pacific Ocean remains an open question. Observational evidence from satellite altimeter shows that low-mode ITs can propagate over 2000 km from the emanating area (Ray and Cartwright, 2001). Utilizing both sea surface height detected by satellite altimetry and a plane wave fit method, Zhao (2014) presented distinct images of ITs (M2 , K1 , and O1 ) propagating over 2 500 km into the WP from the LS. Comprehending the propagation characteristics of ITs is important in understanding the link between local generation and far-field dissipation. Therefore, it is meaningful to address questions regarding the distance that ITs can propagate and the energy attenuation that might occur during the propagation process.
This study investigate the propagation process of ITs using a numerical simulation method. The collection of observational data of ITs in the abyssal ocean can be expensive and insufficient (Liao et al., 2012; Xu et al., 2014). Satellite surveying methods can detect signals on the sea surface over large spatial scales (Tian et al., 2003; Fan et al., 2008); however, the calculation of baroclinic energy is often underestimated. ITs are tidal-frequency motions within the stratified ocean, numerical methods can provide an effective way discerning ocean internal progress with sufficient spatial and temporal resolutions. The generation and evolution of baroclinic tides have been investigated in many studies that have used numerical simulation methods (Carter et al., 2008; Jan et al., 2008; Kang and Fringer, 2012). Niwa and Hibiya (2004) researched the spatial distribution and energy of M2 ITs in the East China Sea. Kerry et al. (2013) discussed the effect of remote generation sites on the barotropic-baroclinic conversion rate of M2 ITs in the Philippine Sea. In a high-resolution global simulation by Shriver et al. (2012), the beams of both diurnal and semidiurnal ITs were identified propagating thousands of kilometers from the LS into the WP. Although it has not been studied numerically, it should be noted that the transmission of the baroclinic energy of diurnal ITs from the LS into the WP is comparable with that of semidiurnal ITs (Alford et al., 2015).
In the work presented here, we conduct threedimensional simulations of (M2 , K1 , and O1 ) ITs propagating into the WP from the LS. According to the numerical results, the different patterns between diurnal and semidiurnal ITs are presented, and IT energy is computed to analyze the energetics during IT propagation. Section 2 introduces the model setup, energy equation used to estimate the energy budget and the validation of barotropic tides. Section 3 provides the simulated results and zonal baroclinic energy flux of ITs driven by three separate tidal constituents, and also analyzes the energy dissipation rate and the vertical structure along a section of the main path. The conclusions are presented in Section 4.
2 METHODOLOGY 2.1 Model descriptionIn this study, the Regional Ocean Modeling System (ROMS) is used to simulate the ITs generated at the LS. ROMS is a three-dimensional, nonlinear, freesurface, primitive equation model with hydrostatic and Boussinesq approximation (Shchepetkin and McWilliams, 2005). To improve computational efficiency, ROMS calculates relatively faster surface gravity waves and relatively slower internal structure separately, using what is known as the split-explicit time-stepping scheme. The wavelength of an IT is much larger than the water depth, and fluid particle movement is primarily horizontal; therefore, most IT models are hydrostatic (Carter et al., 2012). When the horizontal scale of motion is less than the depth, the nonhydrostatic part becomes important, such as internal soliton waves (Vitousek and Fringer, 2011). Hydrostatic ocean models have been used in a number of previous studies researching ITs (Merrifield and Holloway, 2002; Niwa and Hibiya, 2004; Carter et al., 2008; Jan et al., 2008; Rainville et al., 2010; Kerry et al., 2013).
A terrain-following sigma-coordinate system is employed in ROMS. The primary advantage of the s-coordinate is its good representation of bottom boundary flow, which is important in the generation process of ITs. To reduce the pressure gradient error, smoothing of topography is necessary to a certain extent. However, the generation of ITs is sensitive to the topography (Cai et al., 2000), and an improper smoothing method can reduce the peak of underwater ridges significantly (Di Lorenzo et al., 2006). The smoothing method of Niwa and Hibiya (2004) is used in the simulation because it shows good depiction of topographic features when the resolution exceeds 1/30° after identification. Here, the grid resolution of 1/30° is chosen to save on computing resources. The bottom topography is established using the General Bathymetric Chart of the Oceans (GEBCO), which is a combination of one-minute-resolution satellitederived gravity data and ship depth soundings (http://www.gebco.net/). A second moment turbulence closure scheme (MY2.5) is used for vertical mixing (Mellor and Yamada, 1982).
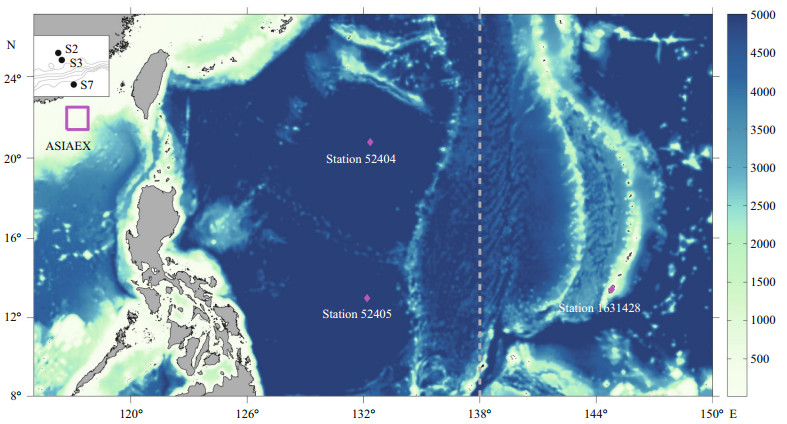
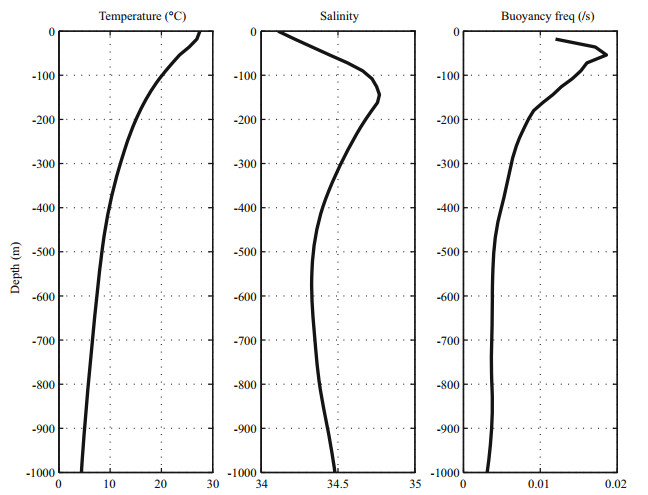
The simulation area with topography is shown in Fig. 1. The background stratification is horizontally uniform and vertically stratified throughout the domain (Fig. 2). The initial temperature and salinity profiles are based on area-averaged (17°–23°N, 120°–135°E) annual mean data from WOA05 (World Ocean Atlas 2005 from the National Oceanographic Data Center), the vertically stratified profile has been spline smoothed to obtain favorable results. The model is driven by surface elevations and barotropic tidal currents derived from TOPEX/Poseidon Global Inver Solution (TPXO7.2) (Egbert and Erofeeva, 2002) at four open boundaries from a state of rest. The Chapman condition (Chapman, 1985) is applied for surface elevation, and the Flather condition (Flather, 1976) and radiation condition are applied for 2-D and 3-D velocities respectively. A 10-cell-wide sponge layer is set along the open boundaries, in which the dissipation coefficients increased exponentially to prevent the reflection of energy back into the simulation area.
|
| Figure 1 Map of the research area with topography The gray dashed line denotes the eastern boundary for the simulation case of M2 ITs. The box of magenta line represents the position of ASIAEX (the inset in the upper left corner shows a closer view). Three magenta diamonds indicate stations in the WP for model verification. |
|
| Figure 2 Area averaged vertical profiles of temperature, salinity and buoyancy frequency |
The energy of the S2 tide is very weak in comparison with the other three major tidal constituents (M2 , K1 , and O1 ); therefore, the analysis of S2 ITs is excluded. Considering that ITs can propagate thousands of kilometers into the WP, generation sites within a certain distance could affect each other. Within the scope of the simulation area, the Mariana Islands arc is another strong source area of M2 ITs except LS, Kerry et al. (2013) indicated that the conversion of M2 ITs at the LS was 11% greater when excluding the effects of remote generation sites (Mariana Islands Arc). Nevertheless, the LS is the dominant source area for diurnal ITs because the Mariana Islands arc does not fulfill the hypothesis of Cacchione et al. (2002). To study the radiation of ITs from the LS into the WP, a relatively small area (set to the east of the boundary at 138°E) is selected for the M2 ITs simulation to reduce the effects of remote generation sites. It requires about 10 days for mode-1 ITs to propagate across the domain; therefore, the model is run for 15 days and results of the final 2 days are used for the analysis.
2.2 Analysis methodsFollowing the baroclinic energy equation given by Kang and Fringer (2012), the baroclinic energy flux is given by
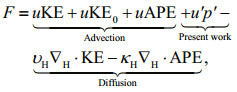 (1)
(1)where KE=ρ0 (u'2+v'2+w2)/2 is the baroclinic kinetic energy (KE), and APE=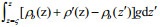
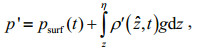 (2)
(2)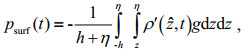 (3)
(3)where υH and κH are the horizontal diffusivity and viscosity, respectively. The baroclinic energy flux is a composition of advection, pressure work, and diffusion terms.
The rate of conversion from barotropic to baroclinic energy is calculated as follows:
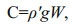 (4)
(4)where W=-∇H ·[(h+η)U] is the vertical barotropic velocity.
2.3 Validation of barotropic tidesForced by a single tidal constituent along the open boundaries separately, tides were reproduced in the simulation area. The simulated results were analyzed harmonically and compared with observed data from six stations within the domain (see Fig. 1). Three of the stations (S2, S3, and S7) of the Asian Seas International Acoustics Experiment (ASIAEX) are distributed in the northern SCS (Beardsley et al., 2004); two stations (Stations 52402 and 52405), maintained by the National Oceanic and Atmospheric Administration (NOAA) National Data Buoy Center, are distributed in the Philippine Sea, and a coastal tidal gauge station (Station 1631428) is deployed in Pago Bay, Guam. The data can be obtained from the NOAA Center for Operational Oceanographic Products and Services website. The absolute RMS error (RMSE) was used to estimate the difference between the simulated results and the practical situation following the definition by Cummins and Oey (1997):
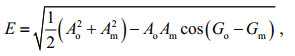 (5)
(5)where A and G represent the amplitude and phase, respectively, and subscripts o and m represent the observed and modeled results, respectively. A comparison of the two sets of results is given in Table 1. The simulated results agreed well with the observations at most stations, although relatively poor agreement was found at Station 1631428. A possible reason for this might be that Station 1631428 is a gauge station on the shore and thus, there was a certain distance between the nearest water grid point and the position of the station. Within the scope of ASIAEX, diurnal tides dominate and provide the energy that generates local diurnal ITs.
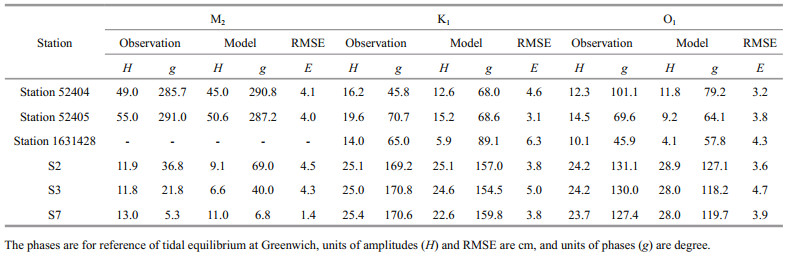
|
The instantaneous distribution of vertical isopycnal displacements for M2 ITs is shown in Fig. 3, relative to the depth of 500 m after 360 hours from the initialization of the calculation. Distinct arc-shaped ripples radiate from a central point at the LS. The amplitudes of the M2 ITs at LS exceed 20 m and reduce to about 5 m at the boundary of the area. The wavelengths of the M2 ITs are about 165 km. In conjunction with the tidal frequency, it can be deduced that the phase speed is about 3.69 m/s, which is consistent with previous estimates by Niwa and Hibiya (2004) (wavelength of 150–200 km; phase speed of 3.5–4.5 m/s). Without the effect of remotely generated ITs, M2 ITs generated at the LS can propagate over 1 500 km into the WP. If the simulation encompassed both the LS and the Mariana Islands arc, the net baroclinic energy flux along the section at 135°E remains eastward (from Fig. 5 in Kerry et al. (2013)). The intensities and directions of ITs can be altered by interference effects and background currents (Rainville et al., 2010; Kerry et al., 2013). The width of the fan-shaped beam increases to thousands of kilometers while propagating forward. For M2 ITs propagating into the SCS, the beam moving northwestward is stronger than that moving southwestward. The northern beam runs onto the continental shelf within a short distance of about three wavelengths, while the southern beam propagates into the SCS basin.
|
| Figure 3 Distribution of vertical isopycnal displacement relative to the depth of 500 m for M2 internal tides, the red curves indicate the main paths of three M2 internal tide beams |
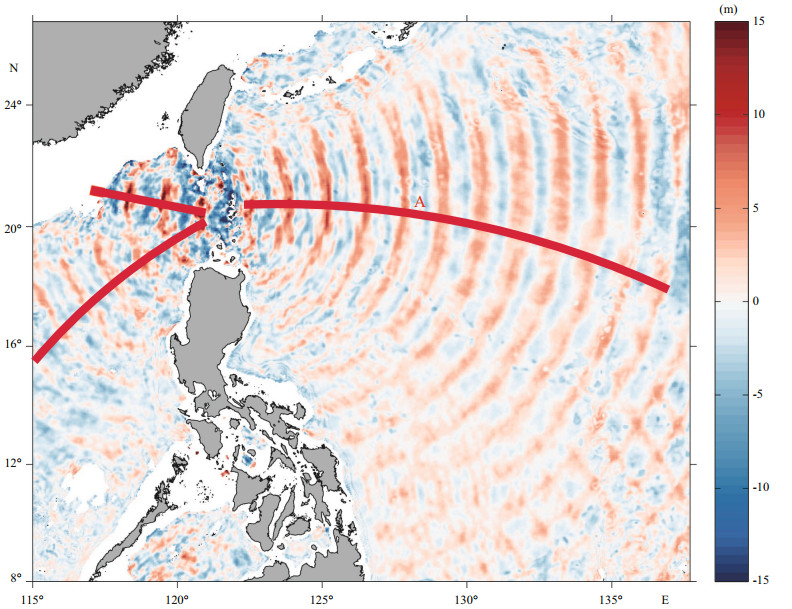
|
| Figure 5 As in Fig. 3 but for a) K1 and b) O1 internal tides |
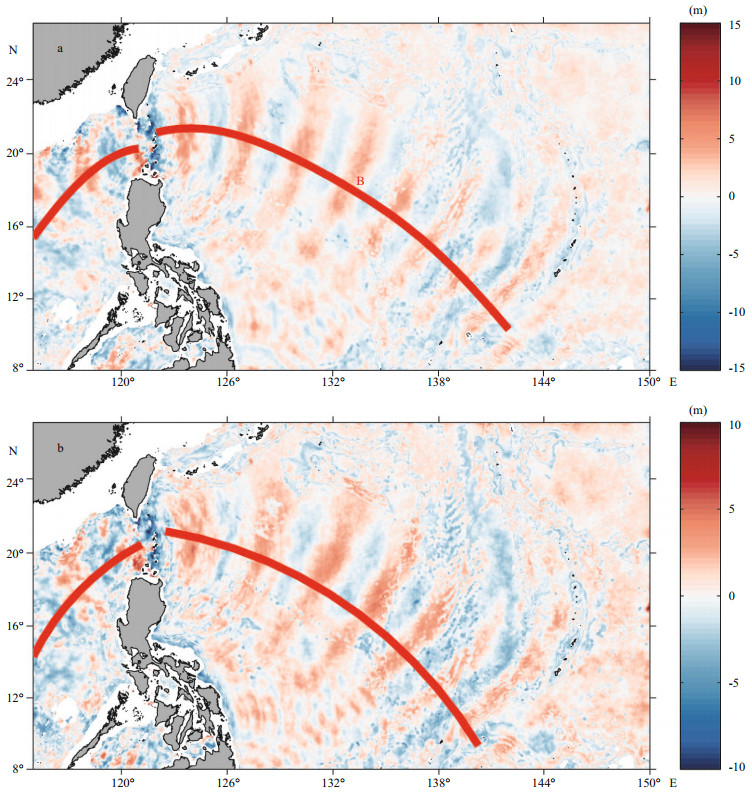
The depth-integrated and period-averaged conversion rate and zonal baroclinic energy flux for M2 ITs are shown in Fig. 4. The flux and conversion rate were computed based on Eqs.1 and 4. M2 ITs generated at the LS propagate both eastward and westward; however, the westward energy flux is greater than the eastward one. ITs that radiate into the WP are generated mainly at the entire eastern ridge and at the western ridge north of 21°N, which is consistent with observation (Alford et al., 2015) and numerical results (Kerry et al., 2013). The westward energy flux shows a north-south asymmetry, which is also revealed by observations (Xu et al., 2014). The eastward energy flux from the LS is concentrated mainly in the center of the LS; the main path of baroclinic energy flux is around 19°–21°N and the width of the zonal energy flux increases during propagation. The intensity of the flux decays slowly as the IT propagates through the deep basin where the topography is more than 3 000 m deep.
|
| Figure 4 Distribution of depth-integrated and period-averaged conversion rate and zonal baroclinic energy flux for M2 internal tides, the 200, 500, 1 000, 2 000, 3 000 and 4 000 m isobaths are shown in light grey |
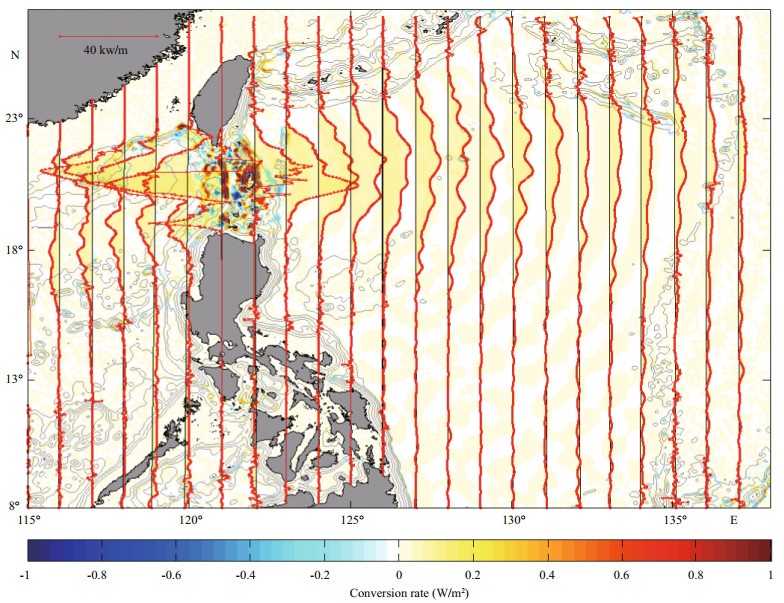
The propagation characteristics have obvious differences between diurnal and semidiurnal ITs. The instantaneous distribution of vertical isopycnal displacements for K1 and O1 ITs are shown in Fig. 5, relative to the depth of 500 m after 360 hours from the initialization of the calculation. The corresponding conversion rate and zonal baroclinic energy flux are shown in Fig. 6. ITs generated at the LS propagate eastward into the WP and westward into the SCS; however, some distinctions can be summarized: (1) the K1 ITs generated at the LS have only two main beams that propagate in the eastward and westward directions. Resulting from the different distribution of the generation area at the LS; (2) K1 ITs have wider beams and larger wavelengths than M2 ITs; (3) unlike M2 ITs, during propagation in the WP, the length of the K1 IT wave-crest line changes slightly and it bends toward the equator. The phase speed of an IT is a function of both latitude and frequency and a greater phase speed occurs at higher latitudes. The difference in phase speeds at different latitudes is more obvious for ITs with lower frequency; (4) because of variable phase speeds, the wavelengths of K1 ITs decrease noticeably when approaching the equator. Most of the conclusions stated here are consistent with satellite results (Zhao, 2014), although further details can be established from the supplementary simulated results. M2 ITs propagating eastward from the LS are generated mainly in the middle of the LS around 21°N; however, for K1 ITs, there exist two peaks for the eastward baroclinic energy flux (separated by 20°N). The local generation of K1 ITs is south of 17°N to the east of the Philippines. This interacts with the ITs from the LS and complicates the internal environment. The zonal baroclinic energy flux of K1 ITs almost vanishes at around 138°E because of the combination of attenuation and the effect of earth's rotation during propagation.

|
| Figure 6 As in Fig. 4 but for K1 internal tides |
A comparison of the instantaneous distribution of vertical isopycnal displacements for K1 and O1 ITs is shown in Fig. 5. The spatial distributions for K1 and O1 ITs are similar but the intensity of the O1 ITs is weaker because of the smaller barotropic amplitude. There are different wavelengths and corresponding phase speeds as a result of the different frequencies. The frequency of the O1 tide is the lowest among the four main tidal constituents, implying the widest distribution of supercritical terrain and multiple generation areas. Consequently, there are more obvious small-scale interactions between locally generated ITs and ITs radiating from the LS. ITs with lower frequency are affected more easily by the earth's rotation and they bend toward the equator (Zhao, 2014). The simulated results are consistent with those derived from satellite altimetry.
3.3 SectionIn accordance with the main propagation paths set in Sections 3.1 and 3.2, two sections in the WP (transect A for M2 ITs in Fig. 3 and transect B for K1 ITs in Fig. 5a) were selected for further study of the along-path structures. Figure 7 shows a cross-section snapshot of zonal velocity and the depth-integrated and period-averaged baroclinic energy (KE plus APE) for M2 ITs. Along the section, the IT beams are clearly visible, reflecting between the thermocline and bottom as they propagate to the right. Low mode ITs dominate after several reflections. At about 1 400 km from the LS, locally generated ITs interact with the ITs propagating from the LS and alter the propagation behavior (Fig. 7a). Signals of M2 ITs generated at the LS can still be detected at a distance of over 1 500 km in the WP (Fig. 7b). In the abyssal ocean of the WP, the attenuation of baroclinic energy is smoother. The along-path baroclinic energy decays to less than 10% beyond 1 000 km from the LS. The wavelength of M2 ITs does not change much (about 165 km) during the propagation process.
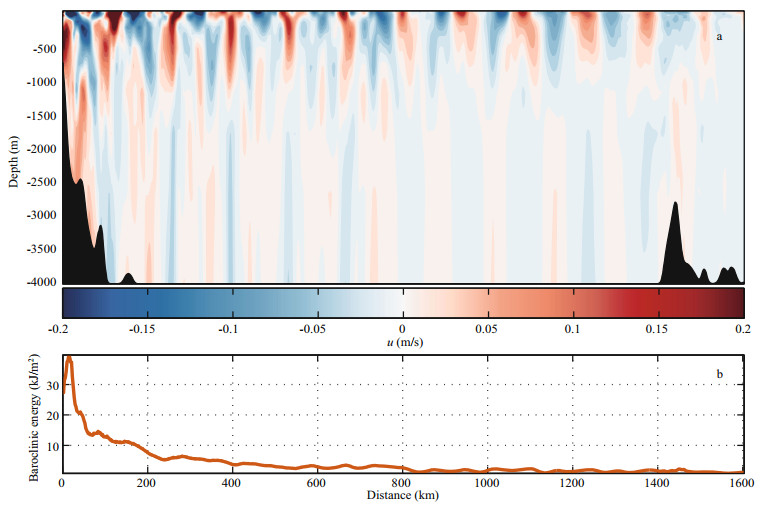
|
| Figure 7 Internal tide beams are indicated by the zonal velocity amplitude of M2 internal tides (a) and depth-integrated and period-averaged baroclinic energy are calculated along the section in Western Pacific (b) distance from the LS are set on the horizontal axis, the unit is kilometers |
The cross-section snapshot of zonal velocity and the depth-integrated and period-averaged baroclinic energy (KE plus APE) for K1 ITs are shown in Fig. 8. Similar ray-like structures alternate along the section, but the wavelengths are larger than M2 ITs, high vertical modes dissipate close to the generation sites. Larger wavelength for diurnal ITs means fewer reflections between thermocline and bottom during propagation, thus diurnal ITs are more capable moving across rough topography. Wavelengths decrease obviously as the distance increase (or rather, as close to the equator). Along the section in WP, signals of K1 ITs can propagate a distance of over 1 800 km, there are also some locally generated ITs along the section (Fig. 8a). In the WP for K1 ITs, the along-path baroclinic energy decay to less than 10% after 1 500 km.
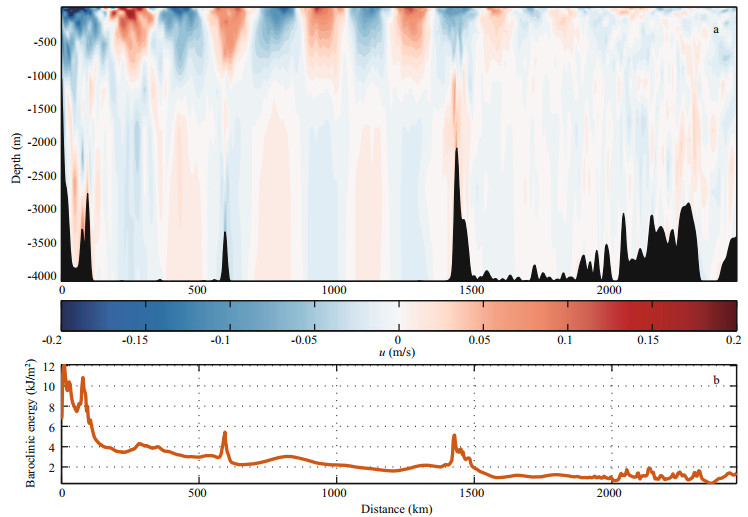
|
| Figure 8 As in Fig. 7 but for K1 internal tides along the section in Western Pacific |
ITs transfer a large amount of energy from their generation sites to the far field, which makes a significant contribution to deep-ocean mixing. In this study, ITs that radiate into the WP from the LS have been investigated using the ROMS high-resolution three-dimensional ocean model, and the simulated ITs are consistent with satellite-derived results. We have analyzed the horizontal distributions of the different tidal constituents (M2 , K1 and O1 ) of ITs in the WP, and the along-path vertical structures and baroclinic energy budget have been investigated as a supplement to the satellite-derived results.
Diurnal and semidiurnal ITs show different patterns and variations during propagation. ITs generated at the LS propagate both eastward and westward, and the westward energy flux is greater than the eastward one. M2 ITs that radiate into the WP are generated mainly in the middle of the LS at around 21°N. However, for K1 ITs, there exist two peaks at the generation site separated by 20°N and these two peaks combine as they propagate eastward. In the WP, ITs generated at the LS can propagate over 1 500 km. ITs with lower frequency are affected more easily by earth's rotation and they bend toward the equator. Phase speed is a function of latitude and stratification; thus, using horizontal uniform stratification in the simulation means that latitude becomes more important. Lower tidal frequencies have greater distinction in phase speed. For M2 ITs in the WP, the width of the beam increases rapidly; however, diurnal ITs bend to the equator as a whole, although the width of the eastward beam does not change much due to the block of land.
Numerical methods complement the description of satellite-derived results in two respects: better estimation of baroclinic energy and demonstration of vertical structures. Along the main propagation path in the WP, high vertical modes vanish near the LS and the first vertical mode dominates after several wavelengths. The estimated depth-integrated and period-averaged along-path baroclinic energy decays to less than 10% after about 1 000 (1 500) km for semidiurnal (diurnal) ITs. The intensity of the baroclinic energy flux dissipates quickly near the generation area and the continental shelf but it decays slowly when propagating in the abyssal ocean. Because of the larger wavelengths and fewer reflections, the energy of diurnal ITs is attenuated more slowly than semidiurnal ITs during the propagation process.
ITs generated at multiple generation sites within a certain distance can interact with each other, and the extent of this effect and the resultant interference patterns have become active areas of research in recent years. To perform a numerical study of ITs radiating into the WP from the LS, strong generation sites other than the LS have been removed (e.g., the Mariana Islands arc for the M2 ITs simulation) and therefore, the simulated results maybe overestimated to some extent. Simulations on the global scale have established the basic internal field, although the resolution is not sufficiently high because of computational expense. The accuracy of simulated ITs could be improved by regional models with finer resolution and better description of topographic features. The Kuroshio Current and its intrusion into the SCS (Hsin et al., 2012) affects the environmental stratification at the LS significantly. The speed of the Kuroshio Current (about 1 m/s) is of the same magnitude as the phase speed of the ITs. Therefore, the Kuroshio Current has great influence on both the generation and the propagation of ITs at the LS. Gaps remain between the simulated environment and the real ocean state, such as the exclusion of atmospheric forcing, using of idealized horizontal uniform stratification, and unsolved dynamics of turbulence dissipation in the model. Further improvement of numeric ocean models is expected in future work.
| Alford M H, MacKinnon J A, Nash J D, et al, 2011. Energy flux and dissipation in Luzon Strait:two tales of two ridges. J.Phys. Oceanogr., 41(11): 2211–2222. Doi: 10.1175/JPO-D-11-073.1 |
| Alford M H, Peacock T, MacKinnon J A, et al, 2015. The formation and fate of internal waves in the South China Sea. Nature, 521(7550): 65–69. Doi: 10.1038/nature14399 |
| Beardsley R C, Duda T F, Lynch J F, et al, 2004. Barotropic tide in the northeast South China Sea. IEEE J. Oceanic Eng., 29(4): 1075–1086. Doi: 10.1109/JOE.2004.833226 |
| Buijsman M C, Klymak J, Legg S, et al, 2013. Threedimensional double-ridge internal tide resonance in Luzon Strait. J. Phys. Oceanogr., 44(3): 850–869. |
| Cacchione D A, Pratson L F, Ogston A S, 2002. The shaping of continental slopes by internal tides. Science, 296(5568): 724–727. Doi: 10.1126/science.1069803 |
| Cai S Q, Chen R Y, Qiu Z, 2000. Numerical study about influence of bottom topographic change on generation of internal tide. Journal of Oceanography in Taiwan Strait, 19(1): 74–81. |
| Carter G S, Fringer O B, Zaron E D, 2012. Regional models of internal tides. Oceanography, 25(2): 56–65. Doi: 10.5670/oceanog |
| Carter G S, Merrifield M A, Becher J M, et al, 2008. Energetics of M2 barotropic-to-baroclinic tidal conversion at the Hawaiian Islands. J. Phys. Oceanogr., 38(10): 2205–2223. Doi: 10.1175/2008JPO3860.1 |
| Chapman D C, 1985. Numerical treatment of cross-shelf open boundaries in a barotropic coastal ocean model. J. Phys.Oceanogr., 15(8): 1060–1075. Doi: 10.1175/1520-0485(1985)015<1060:NTOCSO>2.0.CO;2 |
| Cummins P F, Oey L Y, 1997. Simulation of barotropic and baroclinic tides off Northern British Columbia. J. Phys.Oceanogr., 27(5): 762–781. Doi: 10.1175/1520-0485(1997)027<0762:SOBABT>2.0.CO;2 |
| Di Lorenzo E, Young W R, Smith S L, 2006. Numerical and analytical estimates of M2 tidal conversion at steep oceanic ridges. J. Phys. Oceanogr., 36(6): 1072–1084. Doi: 10.1175/JPO2880.1 |
| Egbert G D, Erofeeva S Y, 2002. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol., 19(2): 183–204. Doi: 10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2 |
| Egbert G D, Ray R D, 2000. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature, 405(6788): 775–778. Doi: 10.1038/35015531 |
| Fan Z S, Zhang Y L, Song M, 2008. A study of SAR remote sensing of internal solitary waves in the north of the South China Sea:Ⅱ.Simulation of SAR signatures of internal solitary waves. Acta Oceanologica Sinica, 27(5): 36–48. |
| Flather R A, 1976. A tidal model of the northwest European continental shelf. Mem. Soc. R. Sci. Liege, 10(6): 141–164. |
| Garrett C, 2003. Internal tides and ocean mixing. Science, 301(5641): 1858–1859. |
| Hsin Y C, Wu C R, Chao S Y, 2012. An updated examination of the Luzon Strait transport. J. Geophys. Res., 117(C3): C03022. |
| Jan S, Lien R C, Ting C H, 2008. Numerical study of baroclinic tides in Luzon Strait. J. Oceanogr., 64(5): 789–802. Doi: 10.1007/s10872-008-0066-5 |
| Kang D J, Fringer O, 2012. Energetics of barotropic and baroclinic tides in the Monterey Bay area. J. Phys.Oceanogr., 42(2): 272–290. Doi: 10.1175/JPO-D-11-039.1 |
| Kerry C G, Powell B S, Carter G S, 2013. Effects of remote generation sites on model estimates of M2 internal tides in the Philippine Sea. J. Phys. Oceanogr., 43(1): 187–204. Doi: 10.1175/JPO-D-12-081.1 |
| Liao G H, Yuan Y C, Yang C H, et al, 2012. Current observations of internal tides and parametric subharmonic instability in Luzon Strait. Atmosphere-Ocean, 50(S1): 59–76. |
| Liu A K, Chang Y S, Hsu M K, et al, 1998. Evolution of nonlinear internal waves in the East and South China Seas. J. Geophys. Res., 103(C4): 7 995–8008. Doi: 10.1029/97JC01918 |
| Liu A K, Su F C, Hsu M K, et al, 2013. Generation and evolution of mode-two internal waves in the South China Sea. Cont.Shelf Res., 59: 18–27. Doi: 10.1016/j.csr.2013.02.009 |
| Ma B B, Lien R C, Ko D S, 2013. The variability of internal tides in the Northern South China Sea. J. Oceanogr., 69(5): 619–630. Doi: 10.1007/s10872-013-0198-0 |
| Mellor G L, Yamada T, 1982. Development of a turbulence closure model for geophysical fluid problems. Rev.Geophys., 20(4): 851–875. Doi: 10.1029/RG020i004p00851 |
| Merrifield M A, Holloway P E, 2002. Model estimates of M2 internal tide energetics at the Hawaiian Ridge. J. Geophys.Res., 107(C8): 5–1. |
| Miao C B, Chen H B, Lü X Q, 2011. An isopycnic-coordinate internal tide model and its application to the South China Sea. Chin. J. Oceanol. Limonol., 29(6): 1339–1356. Doi: 10.1007/s00343-011-1023-5 |
| Niwa Y, Hibiya T, 2004. Three-dimensional numerical simulation of M2 internal tides in the East China Sea. J.Geophys. Res., 109(C4): C04027. |
| Niwa Y, Hibiya T, 2011. Estimation of baroclinic tide energy available for deep ocean mixing based on threedimensional global numerical simulations. J. Oceanogr., 67(4): 493–502. Doi: 10.1007/s10872-011-0052-1 |
| Rainville L, Johnston T M S, Carter G S, et al, 2010. Interference pattern and propagation of the M2 internal tide south of the Hawaiian Ridge. J. Phys. Oceanogr., 40(2): 311–325. Doi: 10.1175/2009JPO4256.1 |
| Ray R D, Cartwright D E, 2001. Estimates of internal tide energy fluxes from Topex/Poseidon altimetry:central North Pacific. Geophys. Res. Lett., 28(7): 1259–1262. Doi: 10.1029/2000GL012447 |
| Shchepetkin A F, McWilliams J C, 2005. The regional oceanic modeling system (ROMS):a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Modelling, 9(4): 347–404. Doi: 10.1016/j.ocemod.2004.08.002 |
| Shriver J F, Arbic B K, Richman J G, et al, 2012. An evaluation of the barotropic and internal tides in a high-resolution global ocean circulation model. J. Geophys. Res., 117(C10): C10024. |
| Simmons H L, Hallberg R W, Arbic B K, 2004. Internal wave generation in a global baroclinic tide model. Deep Sea Res.Part Ⅱ Top. Stud. Oceanogr., 51(25-26): 3043–3068. Doi: 10.1016/j.dsr2.2004.09.015 |
| Tian J W, Zhou L, Zhang X Q, et al, 2003. Estimates of M2 internal tide energy fluxes along the margin of Northwestern Pacific using TOPEX/POSEIDON altimeter data. Geophys. Res. Lett., 30(17): 1889. |
| Vitousek S, Fringer O B, 2011. Physical vs. numerical dispersion in nonhydrostatic ocean modeling. Ocean Modelling, 40(1): 72–86. Doi: 10.1016/j.ocemod.2011.07.002 |
| Xu Z H, Yin B S, Hou Y J, et al, 2013. Variability of internal tides and near-inertial waves on the continental slope of the northwestern South China Sea. J. Geophys. Res., 118(1): 197–211. Doi: 10.1029/2012JC008212 |
| Xu Z H, Yin B S, Hou Y J, et al, 2014. Seasonal variability and north-south asymmetry of internal tides in the deep basin west of the Luzon Strait. J. Mar. Syst., 134: 101–112. Doi: 10.1016/j.jmarsys.2014.03.002 |
| Xu Z H, Yin B S, Hou Y J, 2010. Highly nonlinear internal solitary waves over the continental shelf of the northwestern South China Sea. Chin. J. Oceanol.Limonol., 28(5): 1049–1054. Doi: 10.1007/s00343-010-9018-1 |
| Xu Z H, Yin B S, Hou Y J, 2011. Multimodal structure of the internal tides on the continental shelf of the northwestern South China Sea. Estuarine, Coastal and Shelf Science, 95(1): 178–185. Doi: 10.1016/j.ecss.2011.08.026 |
| Xu Z H, Yin B S, Yang H W, et al, 2012. Depression and elevation internal solitary waves in a two-layer fluid and their forces on cylindrical piles. Chin. J. Oceanol.Limonol, 30(4): 703–712. Doi: 10.1007/s00343-012-1188-6 |
| Zhao Z X, Klemas V, Zheng Q A, et al, 2004. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern South China Sea. Geophys. Res.Lett., 31(6): L06302. |
| Zhao Z X, 2014. Internal tide radiation from the Luzon Strait. J. Geophys. Res., 119(8): 5434–5448. Doi: 10.1002/2014JC010014 |
 2017, Vol. 35
2017, Vol. 35


