Institute of Oceanology, Chinese Academy of Sciences
Article Information
- QI Cailing, RAO Qiuhua, LIU Qi, MA Wenbo
- Traction rheological properties of simulative soil for deep-sea sediment
- Journal of Oceanology and Limnology, 37(1): 62-71
- http://dx.doi.org/10.1007/s00343-018-7258-7
Article History
- Received Oct. 12, 2017
- accepted in principle Feb. 16, 2018
- accepted for publication Apr. 11, 2018
2 School of Civil Engineering, Central South University, Changsha 410075, China;
3 Hunan Key Laboratory of Geomechanics and Engineering Safety, Xiangtan University, Xiangtan 411105, China
Marine mineral resources are regarded as one of the most economically attractive resources in the ocean. It is important to exploit the marine mineral resources to guarantee the sustainable development of human society (Kato et al., 2011; Ma et al., 2017). Many kinds of deep-sea mining systems have been designed for exploiting marine mineral resources, such as continuous bucket mining system, shuttle mining system and hydraulic lifting pipeline mining system (Liang and Wang, 2005). All of these mining systems consist of five main parts: a mining ship, a flexible hose, a buffer, a rigid pipe, and a tracked mining vehicle. In particular, the movement characteristics of the mining vehicle on the seabed play an important role in deep-sea mining operations (Lv et al., 2004; Xu et al., 2018).
The water content of the deep-sea sediment is higher than ordinary land-soil, which causes low shear strength and obvious rheological properties of the soil (Kumar et al., 2010; Mathai et al., 2012). Hence, the mining machines that operate on deep-sea beds can easily slip due to lack traction (Brandes, 2011). With regard to tracked vehicles, there have been various studies of how they interact with land soil. Raymond and Jayakumar (2015) modeled and analyzed track vehicle-soil interactions to compare the mobility of two notional path clearing implements pushed by a tracked vehicle. Arvidsson et al. (2011) compared the tractions of different types of tractors on clay soil. Hemmat et al. (2014) explored the relationships between rut depth, the soil elastic limit (σpc) and average ground pressure (σ) for the unstable calcareous clay. Chandio (2013) studied the traction properties of the grousers with different tooth profiles, water content, and ground pressures by introducing the rheological parameter. Manuwa and Ademosun (2007) researched the influence of some soil water content and cone index on traction. For the deep-sea sediment, Schulte (Schulte et al., 2003; Schulte and Schwarz, 2009), Hong and Choi (2001) and Ma et al. (2015a) established the relative traction models to reflect the interaction between the grouser and the deep-sea sediment. However, the traction rheological properties of soil has been taken into account neither in the studies of land soil nor the deep-sea sediment.
In this study, the best simulative soil was prepared by mixing four different bentonites with a certain percentage of water. The traction rheological tests of the simulative soil were conducted by a home-madetest apparatus under different ground pressures and tractions. The tests are designed to simulate the traction and ground pressure exerted by the mining machine on deep sea sediments due to its weight and movement. A new rheological constitutive model proposed on the basis of fractional derivative theory is used to accurately describe the traction rheological properties and obtain the traction rheological parameters. The relationships between the traction, the velocity and time obtained on the basis of the fractional derivative rheological constitutive equation are intended to predict a suitable ground contact length of track and walking velocity. The two important data can be used to take full advantages of the maximum traction provided by the soil and safely improving mining efficiency.
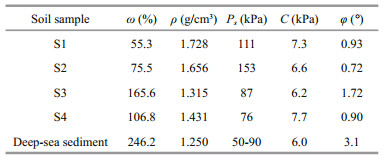
2 TRACTION RHEOLOGICAL TESTS 2.1 Preparation of simulative soilConsidering that it is not possible to meet the requirements of experimental studies using only a small amount of deep-sea sediment, simulative soils have been usually used as substitutes for the deep-sea sediment (Hillenbrand et al., 2003; Maher et al., 2004; Wang et al., 2011; Ma et al., 2014a). Therefore, four kinds of simulative soils, i.e., S1, S2, S3, and S4, were prepared by mixing four kinds of bentonites with a certain percentage of water (Ma et al., 2015a). Table 1 lists the water content ω, the wet density ρ, the penetration resistance Ps, the cohesion C, and the internal friction angle φ of the simulative soil and the deep-sea sediment. It is seen that the S3 simulative soil has the closest physical and mechanical parameters to the deep-sea sediment, and becomes the best substitution for the deep-sea sediment (Ma et al., 2015a).
The traction creep test apparatus shown in Fig. 1 was used to obtain traction creep curves. The S3 simulative soil was prepared to pave in the apparatus, and the grouser (mm, mm) (Xu et al., 2012) was selected to be fixed on the truck. According to the designed ground pressure σ0 of the mining machine (σ0=5 kPa) (Ma et al., 2016), the constant compressive stress was selected as 0 kPa, 5 kPa, and 10 kPa, respectively. The traction was selected according to the maximum traction in each group (Ma et al., 2015). One end of the chain was fixed on the truck, and weights were used to exert a constant traction in the other end to pull the S3 simulative soil. The relationship of the displacement and time was automatically recorded by the NS- WY02 displacement sensor for the displacement-time curves.

|
| Fig.1 Traction properties test apparatus for simulative soil 1. weight; 2. rail; 3. chain; 4. truck; 5. pulley; 6. magnetic stand; 7. NS- WY02 displacement sensor; 8. computer; 9. data mining machine; 10. data display. |
Traction creep curves of the S3 simulative soil under different constant ground pressures and tractions are presented in Fig. 2. It can be seen that all of the curves are divided as three stages: transient creep stage (transient deformation at t=0), unstable creep stage (creep rate is decreased) and stable creep stage (Ma et al., 2014b).

|
| Fig.2 Creep curves under different constant ground pressures and tractions |
A series of curves are shown in Fig. 3. They indicate that the higher the traction force, the larger the transient creep. Hydrophilic minerals, such as montmorillonite, are the main mineral composition of the simulative soil, leading to higher water content (165.6%) and thicker hydrated film of the S3 simulative soil. Therefore, the transient creep is caused by elastic deformation of a large number of hydrated films.
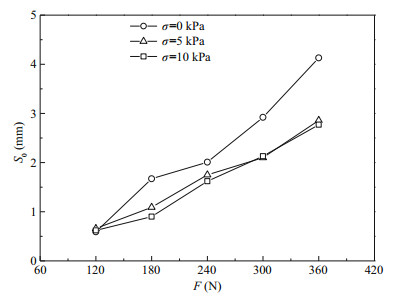
|
| Fig.3 Transient traction creep displacement carrying with ground pressures and tractions |
As time increases, it gradually enters into unstable creep stages. The deformation of the hydrated film (called softening effect) causes the soil particles to be tightly connected and hinders the interparticle movement, which is known as hardening effect. As shown in Fig. 2, when the softening rate and hardening rate reach a dynamic equilibrium (i.e., a stable creep stage), the unstable creep rate gradually reaches a constant value.
As presented in Fig. 4, as the increasing traction, the softening effect is gradually stronger than the hardening effect, and the stable creep rate increases with the increase of traction. Thus the S3 simulative soil has obvious non-attenuation creep properties.
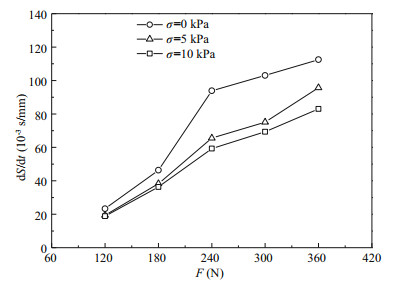
|
| Fig.4 Stable creep rate carrying with ground pressures and tractions |
When the traction is a constant, the transient creep (Fig. 3) and the stable creep rate (Fig. 4) decrease as the increase of the ground pressure. That is because the larger the ground pressure, the more compact the simulative soil, which leads to more difficulty in creep deformation of the simulative soil.
3 TRACTION RHEOLOGICAL MODEL AND PARAMETER DETERMINATION 3.1 Burgers rheological modelBurgers model, which can reflect the nonattenuation creep properties, is commonly used in describing rheological property of soil (Fig. 5). Constitutive equations of spring and dashpot model are rewritten by Eq.1 where stress and strain must be rewritten by traction F and displacement S for test results of S-t curve (Ma et al., 2014b).
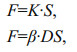 (1)
(1)
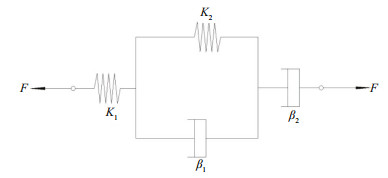
|
| Fig.5 Burgers rheological model |
where K1, K2 are elastic parameters, MPa·mm; β1, β2 a viscous parameters, MPa·s·mm; D=d/dt is first-order of differential operator.
According to the series rule
 (2)
(2)The rheological constitutive equation can be deduced
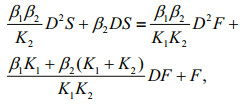 (3)
(3)Therefore, the creep constitutive equation is obtained when F is constant as follows
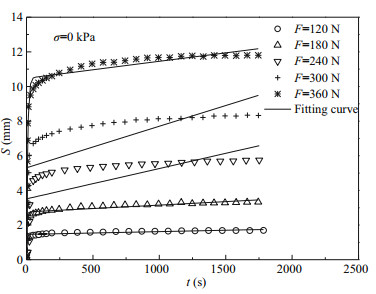
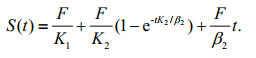 (4)
(4)According to Eq.4, there are large deviations between fitting curves and experimental results (Fig. 6). The minimum and maximum correlation coefficients (R2) are 0.992 8 and 0.603 2, respectively. The average correlation coefficient is only 0.926 4, indicating the Burgers model can not accurately describe rheological properties of simulative soil. The constitutive equation of the Newtonian dashpot is an integer order differential equation representing the ideal fluid. However, the simulative soil is a two-phase medium (solid-liquid coexistence), the mechanical properties of simulative soil lie between the ideal fluid and ideal solid (spring). Therefore, the traditional integer order viscoelastic constitutive model can not be used to describe the mechanical behavior of the simulative soil.
|
| Fig.6 Displacement-time curve fitting of Burgers model |
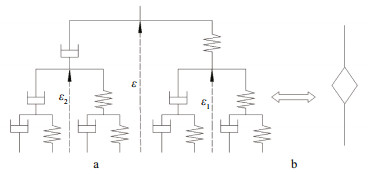
In order to improve the fitting precision of the Burgers model, the Newtonian dashpot in Maxwell body was replaced by a self-similarity spring-dashpot fractance (Schiessel and Blumen, 1993; Heymans and Bauwens, 1994), as shown in Fig. 7. Then, the constitutive equation of fractional derivative Burgers model was established based on fractional derivative theory (Papoulia et al., 2010; Katicha and Flintsch, 2012).
|
| Fig.7 Spring-dashpot fractance (a); fractional element (b) (α=0.5) |
A fractional calculus can be defined by different ways, but the most famous ones of these definitions that have been popularized in the field of fractional calculus are the Riemann-Liouville definition and Grunwald-Letnikov definition. In this study, the Riemann-Liouville definition will be used to describe the rheological properties of the simulative soil (He et al., 2016).
 (5)
(5)where Γ(z) is the Gamma function, i.e., 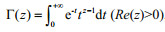
A number of studies (Zhu et al., 2007; Orczykowska et al., 2015; Cajić et al., 2017) have shown that the self-similarity spring-dashpot fractance can be used to describe the material which has both the spring and the Newtonian dashpot properties. According to the Heaviside calculus (Zhu et al., 2007), the constitutive relation of the spring-dashpot fractance is given by
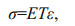 (6)
(6)where E is the elastic modulus of the spring, T is the operator to be solved.
The Eq.6 can be used to describe both a spring in a special case of T=1, and a Newtonian dashpot in a special case of T=(μ/E)D, where μ is the viscosity coefficient of the dashpot, D=d/dt is first-order of differential operator.
According to the series rule, the total stress is the same as components, while the total strain is the sum of the strain of all components. Thus the total strain shown in Fig. 7 can be expressed as
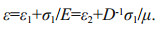 (7)
(7)Due to the self-similarity of the system, Eq.7 can be further rewritten into
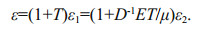 (8)
(8)According to the parallel rule, the total strain is the same as components, while the total stress is the sum of the stress of all components. Thus the total stress can be expressed as
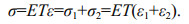 (9)
(9)Combining Eq.8 with Eq.9, we get
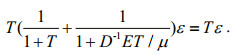 (10)
(10)Namely
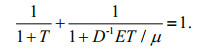 (11)
(11)According to the Heaviside calculus, the operator D can be used as a parameter to participate in algebraic operations. The constitutive operator of the spring- dashpot fractance is obtained from Eq.11.
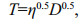 (12)
(12)where η=Eμ, D0.5=d0.5/dt0.5, is the 0.5 order differential operator. Finally, the constitutive relation of the spring-dashpot fractance shown in Fig. 7 is given by
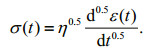 (13)
(13)Considering σ(t)= σ (constant stress) in Eq.13, Eq. 13 is integrated on the basis of the Riemann-Liouville operator, then we obtain
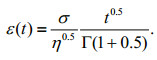 (14)
(14)As shown in Fig. 8, the rheological constitutive equation of the fractional order Burgers model can be deduced
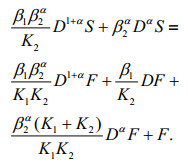 (15)
(15)
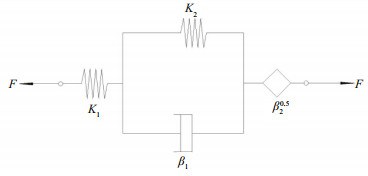
|
| Fig.8 Rheological model of fractional derivative Burgers |
Therefore, when F is a constant, the creep constitutive equation is given by
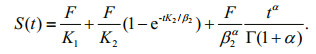 (16)
(16)When α=0.5, Eq.16 can be written as
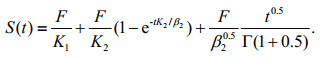 (17)
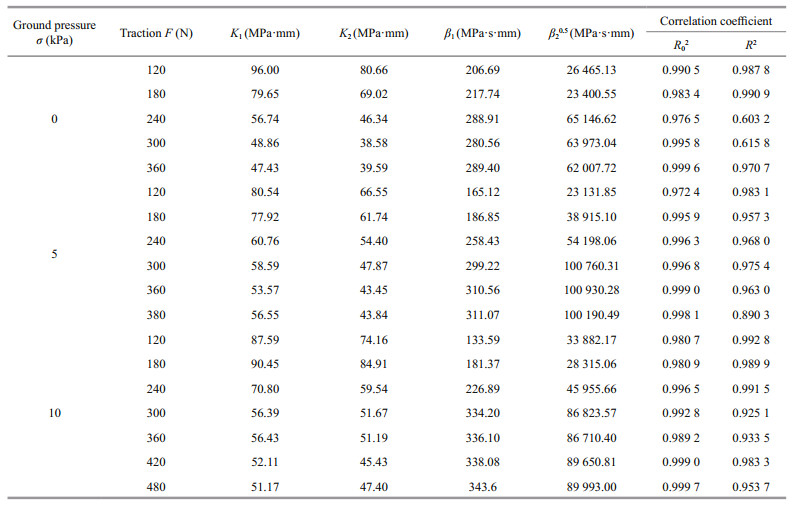
(17)The experimental data as well as the fitting curves fitted by Eq.17 are given in Fig. 9. The traction rheological parameters are listed in Table 2. The minimum, maximum and average correlation coefficients R02 (fractional derivative constitutive model) are 0.999 7, 0.980 7 and 0.991 3, and all of these are greater than R2 (Burgers model), indicating the fractional derivative Burgers model is in better agreement with the experimental data than the Burgers model. Furthermore, the fractional derivative constitutive model proposed in this paper can adequately represent the time-dependent deformation of simulative soil.

|
| Fig.9 Displacement-time curve fitting of the fractional derivative Burgers model |
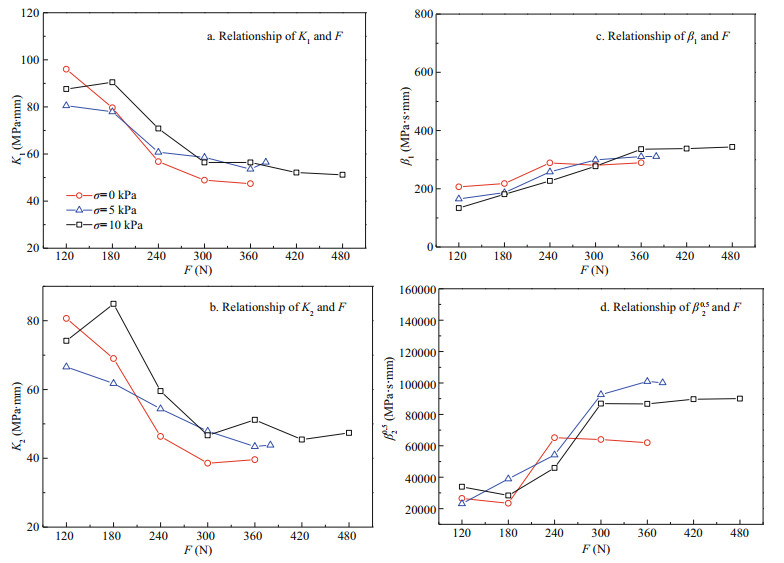
As shown in Fig. 10, rheological parameters vary greatly when F < 300 N, while they stabilize at a constant when F≥300 N. Elastic parameters (K1, K2) decrease with the increase of the traction. Elastic parameters reflect the ability to resist deformation of the soil, and the hydrated film around the soil particle will deform extremely with the increase of the traction, such as break or slipping. Thus the larger the traction, the smaller the elastic parameters. In contrast, viscous parameters (β1, β20.5) increase linearly with the increase of the traction. Viscous parameters, determined by the deformation space, reflect the deformation rate of the soil. The smaller the deformation space, the larger the viscous parameters. With the increase of the traction, soil particles connect more tightly and the deformation space becomes smaller which lead to the viscous parameters increase.
|
| Fig.10 Traction rheological parameters varying with tractions under constant ground pressures |
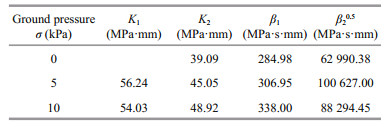
Considering the rheological parameters eventually stand at certain stable values, the rheological parameters of the simulative soil can be determined as average rheological parameters under F≥300 N (Table 3).
When the deep-sea mining machine (designed ground stress σ0=5 kPa) walks on the deep seabed in a constant velocity, namely S=vt, Eq.15 is transformed to
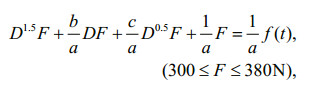 (18)
(18)where 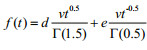
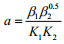
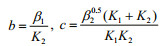
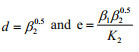
Adomian decomposition method (Adomian, 1989, 1994) is applied to obtain Eq.19
 (19)
(19)Its numerical solution can be achieved by 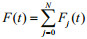
Figure 11 is generated from the numerical solution solved by MATLAB. It indicates the relationship between the traction, the velocity and time. The traction increases with the increase of the working time and the velocity. However, the soil will fail when reaching the strength limit.

|
| Fig.11 raction-time relation varying with constant velocity under σ=5 kPa |
According to the experimental data, the soil will not fail when the traction is lower than 380 N, but the properties of the soil do not stable until F≥300 N. In order to take full advantage of the maximum traction provided by the soil and safely improve mining efficiency, the velocity and the ground contact length of track should be determined on the basis of 300 N≤F≤380 N.
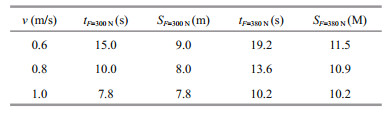
As an example, the following is the predicted velocity and ground contact length of track. When F=300 N and v=0.8 m/s, the time of the track loading on the soil is t=15 s, and the ground contact length of track is S=vt=9 m. As shown in Table 4, range of the ground contact length of track is determined by the time and the velocity required for the traction to reach the maximum and minimum values. It suggests the ground contact length of track stands at 9.0≤S≤10.2 m when the mining machine walks at 0.6≤v≤1.0 m/s.
Traction rheological properties of the simulative soil were studied by a home-made test apparatus. In order to accurately describe the traction rheological parameters, the Newtonian dashpot in Maxwell body of Burgers model was replaced by a self-similarity spring-dashpot fractance and a new rheological constitutive model was deduced by fractional derivative theory. The investigations conducted in this paper lead to the following conclusions:
1) The simulative soil has obvious non-attenuate rheological properties. The transient creep and stable creep rate increase with the traction, but they decrease with ground pressure. By replacing the Newtonian dashpot in Maxwell body of Burgers model with a self-similarity spring-dashpot fractance, the fractional derivative Burgers model are better in describing non-attenuate rheological properties of the simulative soil than the classical Burgers model.
2) For traction rheological constitutive equation of the simulative soil, the traction rheological parameters (K1, K2, β1, β20.5) can be obtained by fitting the tested traction creep data with the traction creep constitutive equation. Though the rheological parameters vary with traction when F < 300 N, they eventually stand at certain stable values, so the rheological parameters of the simulative soil can be determined as average rheological parameters under F≥300 N.
3) Finally, the relationships of traction, velocity and time are obtained based on the traction rheological constitutive equation of simulative soil. The velocity should stand at 0.6≤v≤1.0 m/s and the ground contact length of track should stand at 9.0≤S≤10.2 m, which can take more advantages of the maximum traction provided by the soil and safely improve mining efficiency. It provides an important theoretical basis for designing the deep-sea mining machine.
6 DATA AVAILABILITY STATEMENTThe data that support the findings of this study are available from the corresponding author on request.
7 ACKNOWLEDGMENTThe authors are grateful to the State Key Laboratory of Exploitation and Utilization of Deep-sea Mineral Resources.
Adomian G. 1989. Nonlinear Stochastic Systems Theory and Applications to Physics. Kluwer Academic Publishers, Dordrecht. 309p.
|
Adomian G. 1994. Solution of physical problems by decomposition. Computers & Mathematics with Applications, 27(9-10): 145-154.
|
Arvidsson J, Westlin H, Keller T, Gilbertsson M. 2011. Rubber track systems for conventional tractors-Effects on soil compaction and traction. Soil and Tillage Research, 117: 103-109.
DOI:10.1016/j.still.2011.09.004 |
Brandes H G. 2011. Geotechnical characteristics of deep-sea sediments from the North Atlantic and North Pacific oceans. Ocean Engineering, 38(7): 835-848.
DOI:10.1016/j.oceaneng.2010.09.001 |
Cajić M, Karličić D, Lazarević M. 2017. Damped vibration of a nonlocal nanobeam resting on viscoelastic foundation:fractional derivative model with two retardation times and fractional parameters. Meccanica, 52(1-2): 363-382.
DOI:10.1007/s11012-016-0417-z |
Chandio F A. 2013. Rheological properties of paddy soil under various pressure, water content and tool shapes. American Journal of Agricultural and Biological Sciences, 9(1): 25-32.
|
He Z L, Zhu D Z, Wu N, Wang Z, Cheng S. 2016. Study on time-dependent behavior of granite and the creep model based on fractional derivative approach considering temperature. Mathematical Problems in Engineering, 2016: 8572040.
|
Hemmat A, Yaghoubi-Taskoh M, Masoumi A, Mosaddeghi M R. 2014. Relationships between rut depth and soil mechanical properties in a calcareous soil with unstable structure. Biosystems Engineering, 118: 147-155.
DOI:10.1016/j.biosystemseng.2013.12.006 |
Heymans N, Bauwens J C. 1994. Fractal rheological models and fractional differential equations for viscoelastic behavior. Rheologica Acta, 33(3): 210-219.
DOI:10.1007/BF00437306 |
Hillenbrand C D, Grobe H, Diekmann B, Kuhn G, Fütterer D K. 2003. Distribution of clay minerals and proxies for productivity in surface sediments s of the Bellingshausen and Amundsen seas (West Antarctica)-Relation to modern environmental conditions. Marine Geology, 193(3-4): 253-271.
DOI:10.1016/S0025-3227(02)00659-X |
Hong S, Choi J S. 2001. Experimental study on grouser shape effects on trafficability of extremely soft seabed. Journal of Electroanalytical Chemistry, 361(1-2): 57-63.
|
Katicha S W, Flintsch G W. 2012. Fractional viscoelastic models:master curve construction, interconversion, and numerical approximation. Rheologica Acta, 51(8): 675-689.
DOI:10.1007/s00397-012-0625-y |
Kato Y, Fujinaga K, Nakamura K, Takaya Y, Kitamura K, Ohta J, Toda R, Nakashima T, Iwamori H. 2011. Deep-sea mud in the Pacific Ocean as a potential resource for rare-earth elements. Nature Geoscience, 4(8): 535-539.
DOI:10.1038/ngeo1185 |
Kumar M R A, Kumar S, Mathai T, Chandran S, Rajarama K N. 2010. Geotechnical characteristics of marine sediments in selected sectors off west coast of India vis-a-vis provenances. Marine Georesources & Geotechnology, 28(4): 275-287.
|
Liang L Q, Wang S P. 2005. Research on remote supervisory control system of deep-sea mining collector based on UML. The Ocean Engineering, 23(3): 105-109.
(in Chinese) |
Lv D, He J S, Liu S J. 2004. Current study status of exploiting technology to deep-ocean resource. Mining & Processing Equipment, 32(9): 6-9.
(in Chinese) |
Ma W B, Qi C L, Liu Q, Ding Y H, Zhu W. 2017. Adhesion force measurements between deep-sea soil particles and metals by in situ AFM. Applied Clay Science, 148: 118-122.
DOI:10.1016/j.clay.2017.08.011 |
Ma W B, Rao Q H, Feng K, Xu F. 2015. Experimental research on grouser traction of deep-sea mining machine. Applied Mathematics and Mechanics, 36(9): 1 243-1 252.
DOI:10.1007/s10483-015-1979-6 |
Ma W B, Rao Q H, Li P, Guo S C, Feng K. 2014b. Shear creep parameters of simulative soil for deep-sea sediment. Journal of Central South University, 21(12): 4 682-4 689.
DOI:10.1007/s11771-014-2477-3 |
Ma W B, Rao Q H, Wu H Y, Guo S C, Li P. 2014a. Macroscopic properties and microstructure analyses of deep-sea sediment. Rock and Soil Mechanics, 35(6): 1 641-1 646.
(in Chinese) |
Ma W B, Rao Q H, Xu F, Feng K. 2016. Impact compressive creep characteristics of simulative soil for deep-sea sediment. Marine Georesources & Geotechnology, 34(4): 356-364.
|
Maher K, Depaolo D J, Lin C F. 2004. Rates of silicate dissolution in deep-sea sediment:in situ measurement using 234U/238U of pore fluids. Geochimica et Cosmochimica Acta, 68(22): 4 629-4 648.
DOI:10.1016/j.gca.2004.04.024 |
Manuwa S, Ademosun O C. 2007. Draught and soil disturbance of model tillage tines under varying soil parameters. Agricultural Engineering International, 9(4): 1-17.
|
Mathai T, Rajarama K N, Kumar S, Chandran M S, Kumar M R A. 2012. Geotechnical aspects of clayey sediments off Badagara on the Kerala Coast, India. Marine Georesources & Geotechnology, 30(2): 180-193.
|
Orczykowska M, Dziubiński M, Owczarz P. 2015. Structural analysis of gluten-free doughs by fractional rheological mode. Korea-Australia Rheology Journal, 27(1): 33-40.
DOI:10.1007/s13367-015-0005-0 |
Papoulia K D, Panoskaltsis V P, Kurup N V, Korovajchuk I. 2010. Rheological representation of fractional order viscoelastic material models. Rheologica Acta, 49(4): 381-400.
DOI:10.1007/s00397-010-0436-y |
Raymond J B, Jayakumar P. 2015. The shearing edge of tracked vehicle-Soil interactions in path clearing applications utilizing Multi-Body Dynamics modeling & simulation. Journal of Terramechanics, 58: 39-50.
DOI:10.1016/j.jterra.2014.12.003 |
Schiessel H, Blumen A. 1993. Hierarchical analogues to fractional relaxation equations. J. Phys. A Math. Gen., 26(19): 5 057-5 069.
DOI:10.1088/0305-4470/26/19/034 |
Schulte E, Handschuh R, Schwarz W. 2003. Transferability of soil mechanical parameters to traction potential calculation of a tracked vehicle. In: Fifth ISOPE Ocean Mining Symposium. International Society of Offshore and Polar Engineers, Tsukuba, Japan. p.271-280.
|
Schulte E, Schwarz W. 2009. Simulation of tracked vehicle performance on deep sea soil based on soil mechanical laboratory measurements in bentonite soil. The International Society of Offshore and Polar Engineers, 12(6): 20-24.
|
Wang J Y, Cao W G, Zhai Y C. 2011. Experimental study of interaction between deep-sea sediments and tracks. Rock & Soil Mechanics, 32(S2): 274-278.
(in Chinese) |
Xu F, Rao Q H, Ma W B. 2018. Predicting the sinkage of a moving tracked mining vehicle using a new rheological formulation for soft deep-sea sediment. Journal of Oceanology and Limnology, 36(2): 230-237.
DOI:10.1007/s00343-018-6344-1 |
Xu Y, Wu H Y, Zuo L B. 2012. Influence of shoe tooth height of tracked vehicle on traction performance and its parameter determination. Transactions of the Chinese Society of Agricultural Engineering, 28(11): 68-74.
|
Zhu K Q, Hu K X, Yang D. 2007. Analysis of fractional element of viscoelastic fluids using heaviside operational calculus. In: Zhuang F G, Li J C eds. New Trends in Fluid Mechanics Research. Springer, Berlin. p.506-509.
|
Zhu K Q, Yang D, Hu K X. 2007. Fractional element of viscoelastic fluids and start-up flow in a pipe. Chinese Quarterly of Mechanics, 28(4): 521-527.
(in Chinese) |
 2019, Vol. 37
2019, Vol. 37