Institute of Oceanology, Chinese Academy of Sciences
Article Information
- EL ALAOUI EL FELS Abdelhafid, ALAA Noureddine, BACHNOU Ali
- Use of genetic algorithm in new approach to modeling of flood routing
- Journal of Oceanology and Limnology, 37(1): 72-78
- http://dx.doi.org/10.1007/s00343-018-7293-4
Article History
- Received Nov. 11, 2017
- accepted in principle Feb. 22, 2018
- accepted for publication Mar. 7, 2018
2 Laboratory Applied Mathematics and Informatics, Department of Math and Informatics, Faculty of Science and Technics Gueliz, (P. B. 549), Cadi Ayyad University, Marrakech, Morocco
The modeling of flood propagation is a fundamental approach for studying and understanding the spatialtemporal evolution of a hydrograph in a river or canal. In literature, there are several mathematical methods to model the propagation of a flood in a river. The most used methods are the hydrological method as well as the hydraulic method. The hydrological methods are based on the law of the Conservation of mass, the best known of which is the Muskingum method (McCarthy, 1938), which corresponds to an approximate solution of the hydraulic model of kinematic wave (Cunge, 1969). Nevertheless, the hydraulic methods are not only based on the law of the Conservation of mass but also on The Law of Momentum Conservation. The Hayami model is an efficient tool of hydraulic methods. Indeed, Moussa (1996) and Lerat (2009) showed that the Hayami solution was more efficient than a complete hydrodynamic model on a large scale of real applications.
The simulation of flood propagation according to these models requires specific and numerous data, which generally makes the hydrological studies encountered in practice difficult. It is therefore useful, particularly in the field of hydrology, to have simple and reliable methods for dealing with this problem.
Most of the present work will be devoted to proposing a systemic model consisting of a physicalbased transfer function, close to the simulation level of the flood wave convection-diffusion model (Hayami, 1951; Dooge, 1973). The main advantage of the proposed model is its speed of execution, the simplicity of its mathematical formulation and the identical simulation of the Hayami model. This efficiency and simplicity make of this model a simple modeling tool that can be clearly demonstrated in the development of flood forecasting systems.
The performance of the model simulations is controlled by the identification of their optimal parameters which minimize the distance between observed and simulated flows. Deterministic methods are most often used for the calibration of hydrological models, but they have the disadvantage of converging towards a local optimum, which leads us to opt for more robust and efficient methods of metaheuristic optimization in our study. These methods are the Genetic Algorithm (GA) that have proved their efficiency in optimization in different domains (Poloni et al., 2000; Luo et al., 2012; Mouida and Alaa, 2015).
2 MATERIAL AND METHOD 2.1 Presentation of models 2.1.1 Hayami modelThe Hayami model or the convection-diffusion model is a simplification of the Saint-Venant equations obtained supposing that there are no lateral contributions or losses and that the terms of inertia are negligible in conditions of gravity. We then obtain a non-linear convection-diffusion equation on the flow Q:
 (1)
(1)with x: downstream distance; t: times; C: celerity; D: diffusion coefficient.
In the particular case where C and D are constant over a stream river of a length L, the equation of the scattering wave admits an exact analytical solution (Moussa, 1996) which expressed as follow:
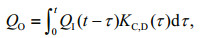 (2)
(2)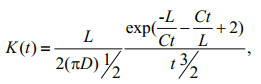 (3)
(3)where QO is the output flow, QI the input flow and L is the length of river.
2.1.2 Proposed modelThe propagation model proposed in this study is based on the systemic approach considering the flood wave as a signal. It establishes a relationship between input and output signals by means of transfer functions (see Fig. 1).
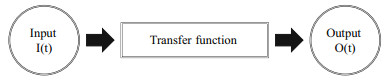
|
| Fig.1 Explanatory diagram of the proposed model |
Procedure of the model is to define the single in output O(t) (downstream flow) as reported entry convolution product of I(t) (upstream flow) and the transfer function f(t), with the function of transfer is a density function of the Gaussian law. The model is defined as follows:
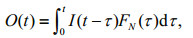 (4)
(4)where
 (5)
(5)In this model, the widening of the impulse response due to convective and diffusive effects is reflected by the density function of the Gaussian law. The Parameter1 represents the duration of the response while Parameter2 represents the delay of the response process after a short variation (pulse) of the input (Pinault and Berthier, 2007).
2.2 Evaluation of modelsWhichever hydrological model is used, it only allows a simplified representation of the hydrological processes, and thus refers to results that are more or less close to reality. It is therefore necessary for the hydrologist to know the margin of uncertainty associated with the simulations of the flows carried out by the model, which makes it possible to evaluate the performance of the latter.
Models are evaluated through the use of performance criteria. These criteria are often statistical methods that aim to standardize the comparison between simulation or forecast results and observations, i.e. they give an idea of the ability of the model to replicate the response of interest. Detailed descriptions of these criteria can be found in the works of Nash and Sutcliffe (1970), Beven and Binley (1992) and Franchini et al. (1996). To quantify the performance of models, there is no universal criterion for evaluation. Many criteria are used in hydrology to assess the sensitivity of the models, including: Root mean square error (RMSE), Mean Bias Error (MBE), Nash…
In this study, we adopted the Nash criterion proposed by Nash and Sutcliffe (1970). This criterion (which we will call the Nash-Sutcliffe criterion or Nash criterion), varying in the interval [-∞; 1] has the advantage of being easy to interpret and emphasizing errors in high flow rates. A criterion of value 1 means that the error of the model is null (perfect model). Kachroo (1986) gave the following scale when the values taken by the Nash criterion:
90% the model is excellent;
80% to 90%, the model is very good; 60% to 80%, the model is good;
less than 60% the model is bad.
This Nash Evaluation Criterion Model defined by the Eq.6 is widely used in hydrology, probably because of its simplicity and its intrinsic link with linear regression.
 (6)
(6)with: Qobs: observed flow; Qsim: simulited flow; Qm: average flow.
2.3 Sensitivity of model's parametersParameters are identifiers of the model that characterize a given environment. They vary depending on the model's use. The identification of the optimal values of the parameters is based on the determination of the range of sets of the latter so that they can be representative of the hydrological behavior studied. With the sensitivity analysis, we are rather interested in exploring the ideal "vicinity" of an optimal solution.
The sensitivity of the model consists in varying the values of the parameters in two finite dimensions and then calculating the value of the evaluation function Nash for each pair of parameters (Parameter1, Parameter2). Then it becomes possible to represent surfaces of iso-value of the latter (Fig. 2). It shows that the sensitivity analysis of the Nash function in comparison to the variations of the model's parameters makes it possible to consider not only an optimal value of the parameters, but also an interval in which their combination gives acceptable simulations. It also allows us to draw the degree of influence of each parameter on the response of the model.
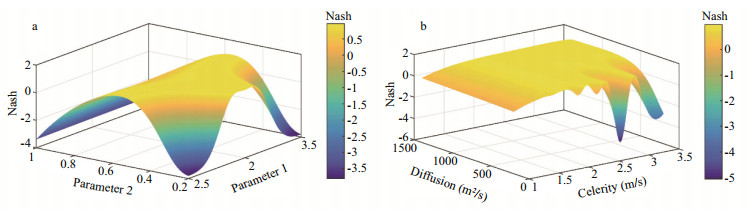
|
| Fig.2 Sensitivity parameters of the proposed model (a); sensitivity parameters of the Hayami model (b) |
The Fig. 2 analysis makes it possible to extract the best intervals of the parameters that control the correct answers of the proposed model. It is noted that the high Nash values are recorded for intervals varying between [2.75; 3.2] of Parameter1 and [0.4; 0.8] of Parameter2, other words the performance of the model translated by the criterion Nash decreases while going away from the intervals of parameters mentioned before. It is also observed that the response of the model is strongly sensitive to the variation of the two parameters at the same time. For the Hayami model, the performance of the model increases depending on the increase of the celerity, concluding that the high Nash are marked for a celerity that exceeds 2.5 m/s and less than 3.5 m/s, but the diffusion coefficient has a low influence on the response of the model, which makes the determination of a precise interval difficult. This sensitivity study shows that the parameter related to the Floods' propagation speed strongly influences the performance of the modeling of observed flood. It should be noted that this sensitivity study is based on real data flood of the N'Fis basin river (site of application of the model), which reveals that the sensitivity study in different sites would lead to other results.
2.4 Mechanism of optimization of the parameters by the Genetic AlgorithmThe Genetic Algorithm (GA) is a research algorithm that is part of a family of evolutionary methods, based on Darwin's theory of natural evolution of species. It combines a strategy of "survival of the strongest" with a random but structured exchange of information. For a problem for which a solution is unknown, the algorithms manipulate a set of possible solutions created randomly in a search space, called population of individuals. The desired variables or (the characteristics) are then used in gene sequences which will be fused with other genes to form chromosomes and subsequently individuals. Each solution is associated with an individual, and this individual is evaluated and classified according to its resemblance to the best solution to the problem.
The basic mechanism of GA consists of three simple operations inspired by the theory of evolution that are no more complicated than algebraic operations: selection, crossing and mutation. The algorithm is defined as follows
Algorithm:
Initialize the population (randomly generate a population of n individuals f(Parameters))
Calculate the degree of adaptation f(Parameters) of each individual
As a non-finished or non-convergence
Select 2 individuals to the times for the reproduction
Apply the genetic operators (crossing, mutation)
Keep only the best individuals
Calculate the degree of adaptation f(Parameters) of each child
Select the survivors among parents and children
End as long as Find the best optimum.
3 RESULT AND DISCUSSION 3.1 Numerical experimentsIn numerical experiments, we want to test the capacity of the proposed model to simulate flood wave propagation. This simulation is based on data generated by the Hayami model, the use of the latter is mainly to have the closest to reality flood characteristics which are generally distinguished by celerity (speed of propagation) and a rate of attenuation or damping.
Numerical validations are based on two points. First, create four scenarios of downstream floods by the Hayami model based on a flood generating virtually upstream. Second, calibrate the proposed model by optimizing the parameters in each scenario.
Each scenario is indicated by an upstream flow and a downstream flow calculated by the Hayami model, while varying the parameters, the celerity C, the diffusion coefficient D and the distance L which separates the measurement points from the downstream and upstream flood.
The calibration of the proposed model come down to the resolution of an optimization problem. This optimization method attempts to minimize the cost function (7) which measures for each set of parameters generated by the Genetic Algorithm the difference between the predictions of the proposed model and the calculated response of the Hayami model.
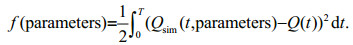 (7)
(7)The model predictions are obtained by numerical simulations (response calculated in Fig. 3a). The process stops when the cost function is less than a fixed value determined before in the program where the number of iterations (generations) is reached (Fig. 3b). The corresponding parameter set is then the desired parameter set. The results obtained show that for the various scenarios, the proposed model is able to simulate perfectly the response calculated by the Hayami model and that the Genetic Algorithm represents a remarkable efficiency in terms of convergence to an optimal solution (expressed by Nash criterion) of the optimization problem.
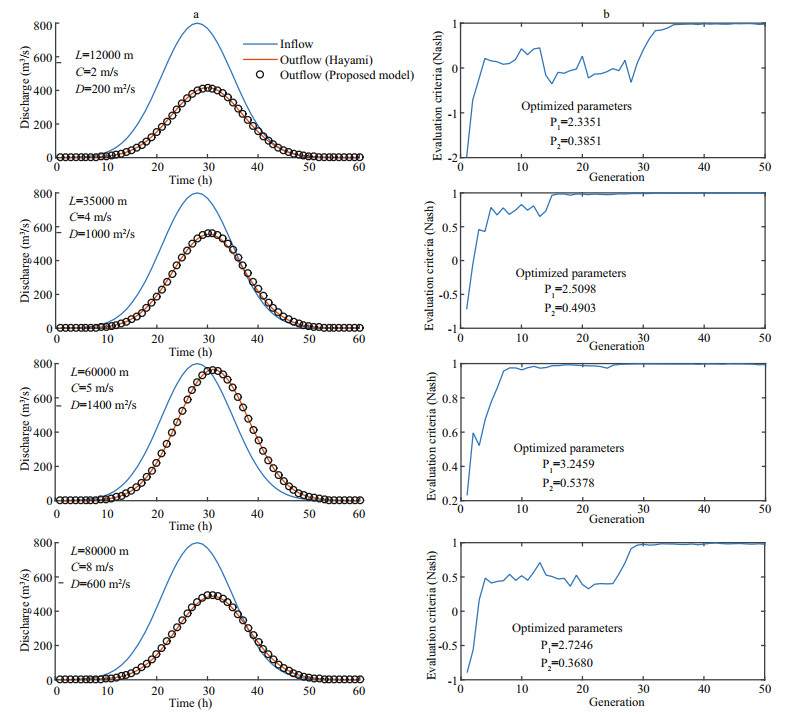
|
| Fig.3 Simulation of the response of Hayami model by the proposed model (a); evolution of Nash criterion by generations (b) |
In order to illustrate the applicability of the proposed model, it is used hereinafter on a real case. The N'fis River, located in the High Atlas Occidental (Morocco), presents elements that appear a priori favorable to the study of the propagation. The data used for our study are provided by the Hydraulic Basin Agency of Tensift. They are the instantaneous hourly flows measured at the two hydrometric stations Imine El Hammam (downstream Station) and Iguir N'kouris (upstream station) (Fig. 4).
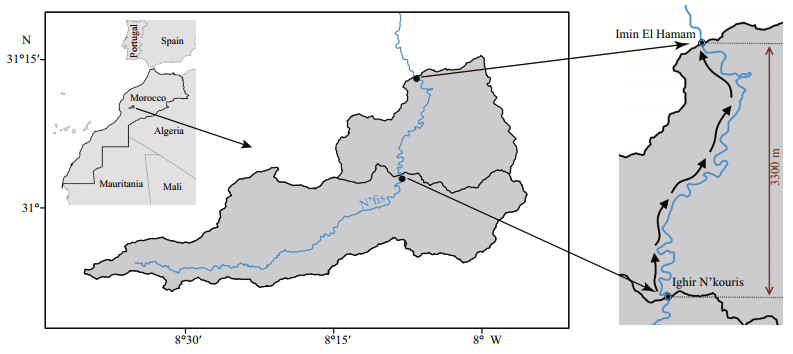
|
| Fig.4 Geographic location of hydrometric stations |
Model calibration is a complex modeling task, requiring the identification of the optimal parameters which gives the minimal error between observed and simulated flows. Deterministic methods are most often used in this modeling phase, but they have the disadvantage of being able to converge towards a local optimum, for this reason we chose the GA as a method of optimizing the parameters of our models in order to avoid the difficulties of classical methods.
The impact of optimized parameters on the simulated hydrograph can be assessed visually and numerically. The visual method consists in comparing for each event the shape of the hydrograph of the simulated flood with the form of the flood hydrograph observed. The numerical method relies on the maximization of Nash evaluation criteria which reflects the correct calibration of the models.
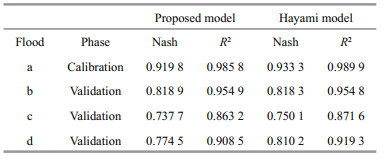
The results obtained from the calibration and the validation are presented in the Fig. 5. Table 1 summarizes the optimized parameters of the models; the Table 2 summarizes the numerical evaluation results. The phase of the calibration shows that both models are able to simulate well the observed flows with an average Nash criterion of 0.92 and a correlation that exceeds 98%.
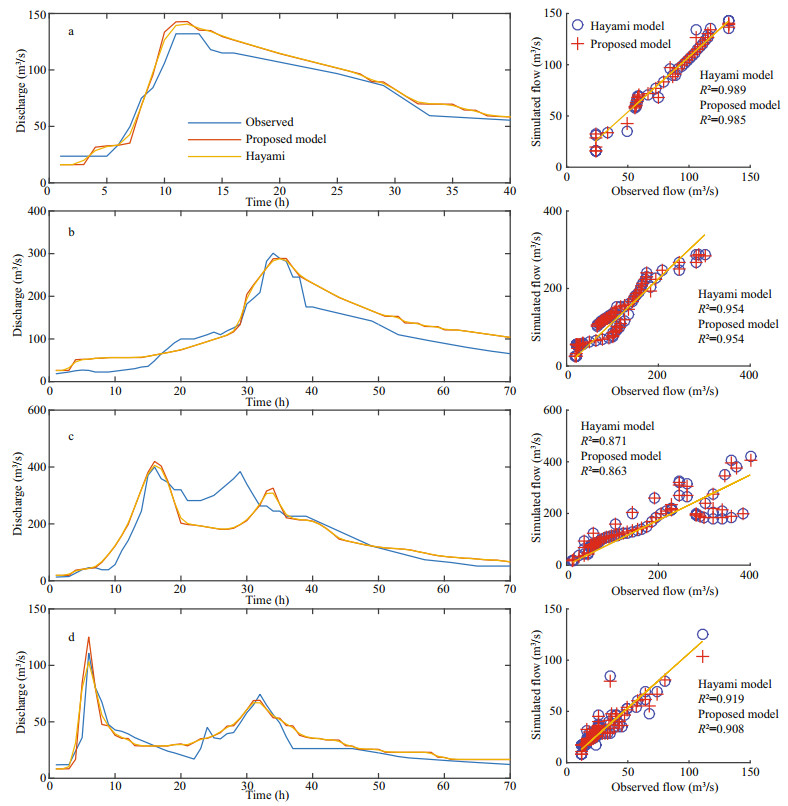
|
| Fig.5 Calibration and validation of the Hayami and the proposed model |
For an unregulated watershed, the Nash value obtained for both models is considered very satisfactory.
When the calibration of the models is completed and judged to be satisfactory according to the Nash evaluation criterion, a validation is carried out. Compared to calibration, the validation consists of a simulation involving different floods but with the same parameter values optimized to verify the quality of the validation. The analysis of the results shows that the simulations carried out by the parameters of the calibration phase are generally acceptable. The forms of the flood hydrographs (b and d) are well adjusted with an average Nash of 0.8 and a correlation of 0.9. The shift recorded in the right part of the flood hydrograph (b) can be explained by the lateral contributions that are not taken into account in the modeling of flood propagation. For the simulated hydrograph of the flood (c), there is an underestimation of flows at the second peak of the hydrograph with an average Nash of 0.74, the only explanation for the shift of the second peak of the hydrograph is that this complex flood is due to two rainy episodes. The first episode is concentrated only in the upstream part of the basin, thus registering a time lag between the upstream and downstream stations of the first peak, whereas the second is a generalized rain event throughout the basin. In other words, the flow rate rise at the second peak is recorded simultaneously time in the downstream and upstream station.
The analysis of the results obtained either in the calibration phase or in the validation phase shows a simulation which can be considered similar for both models despite the mathematical difference of the models.
4 CONCLUSIONThe work proposed in this study allows developing a new simple model in which the applications are easy to implement. The numerical experiment based on the simulation of the calculated response of the Hayami model shows that the capacity of the model to simulate the properties Physics (celerity, diffusion) of a flood wave is very satisfactory. This performance at the simulation level is based on the identification of optimal parameters by the GA of the proposed model. The applicability of this model to actual flood data has yielded very encouraging results. Despite the good results obtained, this work requires other deep studies that not only have a good simulation of the hydrological response of the Hayami model but also have a mathematical relationship that binds the parameters of the elaborated model and those of the Hayami model. Compared to this model, the proposed one has the advantage of the simplicity of its mathematical formula in addition to its ability to simulate the hydrodynamic properties of flood propagation. However, it would be adapted only for a limited case whose side flow contributions are negligible.
Beven K, Binley A. 1992. The future of distributed models:model calibration and uncertainty prediction. Hydrological Processes, 6(3): 279-298.
DOI:10.1002/(ISSN)1099-1085 |
Cunge J A. 1969. On the subject of a flood propagation computation method (Muskingum method). Journal of Hydraulic Research, 7(2): 205-230.
DOI:10.1080/00221686909500264 |
Dooge J C I. 1973. Linear Theory of Hydrologic Systems.Technical Bulletin no. 1468, USDA, Washington, DC, USA.
|
Franchini M, Wendling J, Obled C, Todini E. 1996. Physical interpretation and sensitivity analysis of the TOPMODEL. Journal of Hydrology, 175(1-4): 293-338.
DOI:10.1016/S0022-1694(96)80015-1 |
Hayami S. 1951. On the propagation of flood waves. In: Bulletin-Disaster Prevention Research Institute. Kyoto University, Kyoto, Japan.
|
Kachroo R K. 1986. HOMS workshop on river flow forecasting, Nanjing, China. Unpublished internal report, Dep. Eng.Hydrol., University College Galway, Galway, Ireland. 149p.
|
Lerat J. 2009. Quels apports hydrologiques pour les modèles hydrauliques? Vers un modèle intégré de simulation des crues. Université Pierre et Marie Curie, Paris, French. (in French)
|
Luo Q K, Wu J F, Sun X M, Yang Y, Wu J C. 2012. Optimal design of groundwater remediation systems using a multiobjective fast harmony search algorithm. Hydrogeology Journal, 20(8): 1 497-1 510.
DOI:10.1007/s10040-012-0900-0 |
McCarthy G T. 1938. The unit hydrograph and flood routing.In: Proceedings of Conference of North Atlantic Division.U.S. Army Corps of Engineers, Wahsington, DC.
|
Mouida A, Alaa N E. 2015. Non-domination sorting genetic algorithm Ⅱ for optimization of Priestley-Taylor transpiration parameters. Annals of the University of Craiova, Mathematics and Computer Science Series, 42(1): 3-12.
|
Moussa R. 1996. Analytical Hayami solution for the diffusive wave flood routing problem with lateral inflow. Hydrological Processes, 10(9): 1 209-1 227.
|
Nash J E, Sutcliffe J V. 1970. River flow forecasting through conceptual models part Ⅰ-a discussion of principles. Journal of Hydrology, 10(3): 282-290.
DOI:10.1016/0022-1694(70)90255-6 |
Pinault J L, Berthier F. 2007. A methodological approach to characterize the resilience of aquatic ecosystems with application to Lake Annecy, France. Water Resources Research, 43(1): W01418.
|
Poloni C, Giurgevich A, Onesti L, Pediroda V. 2000. Hybridization of a multi-objective genetic algorithm, a neural network and a classical optimizer for a complex design problem in fluid dynamics. Computer Methods in Applied Mechanics and Engineering, 186(2-4): 403-420.
DOI:10.1016/S0045-7825(99)00394-1 |
 2019, Vol. 37
2019, Vol. 37