Institute of Oceanology, Chinese Academy of Sciences
Article Information
- YUAN Shijin, ZHANG Huazhen, LI Mi, MU Bin
- CNOP-P-based parameter sensitivity for double-gyre variation in ROMS with simulated annealing algorithm
- Journal of Oceanology and Limnology, 37(3): 957-967
- http://dx.doi.org/10.1007/s00343-019-7266-2
Article History
- Received Sep. 23, 2017
- accepted in principle Jan. 7, 2018
- accepted for publication Aug. 3, 2018
The double gyre, which consists of a sub-polar gyre and a sub-tropical gyre, is a typical phenomenon of large-scale ocean circulation in the northern midlatitude ocean basins (Shen et al., 1999). The double gyre has the important guiding significance in understanding the nonlinear dynamics of windinduced circulation (Jiang et al., 1995; Simonnet et al., 2005), especially the dynamic behaviors of western boundary currents (Mahadevan et al., 2001; Primeau and Newman, 2008; Zhang et al., 2015).
The double gyre shows a low-frequency variation which is associated with the transition of the midlatitude ocean circulation (Nauw and Dijkstra, 2001), the study of double-gyre variation is helpful to improve the prediction skills of mid-latitude ocean circulation. Many models such as Regional Ocean Modeling System (ROMS) which is a complex multilayer model, can be used to simulate double-gyre variation. While using a model for simulation, the simulation is mainly influenced by initial condition (Mahadevan et al., 2001; Van Scheltinga and Dijkstra, 2008; Yuan et al., 2016) and model parameter (Moore, 1999; Primeau, 2002; Nauw et al., 2004). The research problem for prediction associated with model parameter is called second kind of predictability problem which is important to study predictability of double gyre.
Model parameter values can greatly influence model results (Hamby, 1994) and unknown model sensitivity to parameters are major limitations to global and regional modeling (White et al., 2000). Many experiments had pointed out that reducing the error of model parameters can reduce the uncertainty of models and improve the prediction skills (Lu and Hsieh, 1997, 1998; Zaehle et al., 2005). Different parameters of model have different sensitivities (bhall et al.1998; Hall et al., 1982; Navon, 1998), determining sensitive parameters and then reducing the error of the sensitive parameters can effectively reduce the uncertainty of the model prediction (Yin et al., 2014). In this paper, we study the parameters sensitivity for double-gyre variation in ROMS.
There were many researches on the parameters of double gyre variation. For example, some researchers (Moore, 1999; Sura and Penland, 2002; Pierini, 2010; Sapsis and Dijkstra, 2013) analyzed the influence of wind stress on the double gyre variation. Primeau et al. (Primeau, 2002; Primeau and Mewman, 2008) studied the influence of parameters such as viscosity coefficient and wind stress on the multiple equilibria and lowfrequency variability of the double gyre in the quasigeostrophic model and shallow-water model respectively. Nauw et al. (2004) analyzed the influence of lateral friction on the asymmetry of double gyre in a 1.5-layer shallow-water model. However, these works were only performed in simplified models and did not take the influence of barocline into account. Meanwhile, the sensitivity of the combination of multiple parameters wasn't addressed. For doublegyre variation simulation in ROMS, according to the previous researches, we study the sensitivity for wind amplitude (WD), viscosity coefficient (VC) and linear bottom drag coefficient (RDRG), which correspond to wind stress, viscosity coefficient and lateral friction respectively. In addition, we not only study the sensitivity of the single parameter, but also the combination of multiple parameters.
Mu et al. (2010) proposed Conditional Nonlinear Optimal Perturbation related to Parameter (CNOP-P) method to assess the effects of parameter uncertainties. Subsequently, Yin et al. (2014) and Sun et al. (2017) applied the CNOP-P method to investigating the parameters sensitivity in the Lorenz-63 model and LPJ model (Lund-Potsdam-Jena model), which implies that CNOP-P method is an effective method for the study of parameters sensitivity.
Solving CNOP by the intelligent algorithm has been widely applied to exploring the El Niño-Southern Oscillation (ENSO) event's optimal precursor and the fastest growth initial error in Zebiak-Cane (ZC) model (Wen et al., 2015; Yuan et al., 2015a, 2015b; Ren et al., 2016), to carry out tropical cyclone adaptive observations in Fifth-Generation Penn State/NCAR Mesoscale Model (MM5) (Zhang et al., 2017) and to obtain the optimal precursor of double gyre variation in ROMS (Yuan et al., 2016). These applications indicate the effectiveness of the intelligent algorithm in solving CNOP. And for the purpose of more effectively solving CNOP-P of ROMS, we introduce some strategies to SA algorithm (Kirkpatrick et al., 1983) to find the optimal solution more effectively.
In this paper, we study the sensitivity of the parameters for WD, VC and RDRG based on CNOP-P method in double-gyre variation simulation of ROMS, including the sensitivity of the single parameter and the combination of multiple parameters. In addition, an improved simulated annealing (SA) algorithm was proposed to solve CNOP-P. The rest of paper are organized as follows. After reviewing ROMS and CNOP-P method and introducing the SA algorithm used in the experiment in Section 2. The overview, results and discussions of experiment are shown in Section 3. Finally, conclusions and a prospect to future works are given in Section 4.
2 MATERIAL AND METHOD 2.1 Related works 2.1.1 ROMSROMS is a free-surface, terrain-following, primitive equation ocean model which is widely used in a variety of applications of scientific community (Haidvogel et al., 2000; Marchesiello et al., 2003; Wilkin et al., 2005). Its design follows conventions of ESMF (Earth System Modeling Framework) for model coupling, which is divided into three steps— initialize, run and finalize. It can be used to simulate the global waters of any size from oceans to basins.
The four models, Nonlinear Model (NLM), Tangent Linear Model (TLM), Representer Tangent Linear Model (RPM), Adjoint Model (ADM), compose the dynamical kernel of ROMS. Each model can be run separately or together by the drivers of ROMS. Only NLM is adopted in our experiment. The algorithms of NLM were described in detail in Shchepetkin and Mcwilliams(2003, 2005).
In the simulation of double gyre, following Moore et al. (2004), the model is configured as a flat-bottom rectangular ocean basin with meridional distance of 1 000 km, latitudinal distance of 2 000 km, and vertical height of 500 m which is divided into four vertical levels with a thickness of 125 m. ROMS equations are solved on a mid-latitude β-plane with a horizontal resolution of 18.5 km. Since the WBS extension generally appeared in the district of 35°N or so, we configure the latitude center as 30°N in order to simulate better. The model circulation is mainly forced by a zonally uniform, the form of zonal wind stress is τx=-τ0cos(2π/Ly), where τ0=0.05 N/m2 and Ly is the meridional extent of the basin.
2.1.2 CNOP-PCNOP is a type of initial perturbation in the nonlinear dynamical system proposed by Mu et al. (2003), which satisfies certain constraints and has the maximum nonlinear development at the predicted time. It has become an effective method to measure the predictability of the dynamical system because of the characteristic of possessing the maximum nonlinear development at the predicted time. Mu et al. (2010) extended the CNOP method to the model parameters called CNOP-P to study the influence of parameter perturbation on predictability. The idea of the CNOP-P is as follows.
Let the evolution equations for the state vector X be as follows:
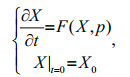 (1)
(1)where t is time, X0 is initial state, p=(p1, p2, ∙∙∙, pm)T is model parameters vector, F is a nonlinear differential operator. Assuming that initial state vector X0 is known exactly, the future state vector Xt at time t can be determined by integrating Eq.1. Therefore, Eq.1 can be written as:
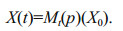 (2)
(2)Here Mt(p) is the nonlinear propagator with parameter vector p, which "propagates" the initial state vector X0 to the time t in the future.
Assuming that superimposing a parameter error p' on the Eq.2, the equation can be written as:
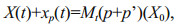 (3)
(3)where xp(t) is the deviation from the reference state X(t) at the predicted time t after p' has been superimposed. In general, the uncertainty of model parameters is caused by parameterization and the values of these parameters are determined by observation. Therefore, these parameters need to satisfy some certain constraints. In order to explore the parameter error under given constraints that can cause the model development to deviate maximally from the reference state at the predicted time, we define a nonlinear optimization problem:
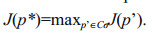 (4)
(4)Here p'∈Cσ describes the parameters constraint, Cσ usually expresses as Cσ={p'=(p1', p2', ∙∙∙, pm'), //p1'//≤σ1, //p2', //≤σ2, ∙∙∙, //pm'//≤σm}. And the objective function is defined as:
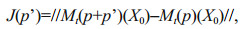 (5)
(5)where Mt(p+p')(X0)–Mt(p)(X0) is degree of deviation xp(t), the specific form of the objective function needs to be defined in conjunction with specific research questions. And the solution p* of Eq.4 is CNOP-P. It can be seen that CNOP-P represents the parameter perturbation that can cause the maximum prediction error under given constraints.
In this experiment, we mainly focus on three parameters—VC, WD, RDRG. Therefore, p and p' in Eq.5 are both composed of these three components, which can be expressed as:
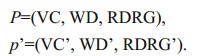 (6)
(6)The area of the simulation of double gyre in ROMS is 0 km≤x≤1 000 km, 0 km≤y≤2 000 km, where x represents the longitudinal distance coordinate and y represents the latitudinal distance coordinate. The objective function is defined as the energy norm where xt is in the region Ʌ (0 km≤x≤600 km, 750 km≤y≤1 250 km), which contains the west boundary of double gyre and the area where jet strongly acts with vortex, that is:
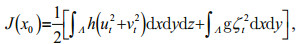 (7)
(7)where h is the thickness of seawater for each layer (each layer of 125 m and a total of 4 layers), g (9.8 m/ s2) is gravity acceleration.
2.2 SA algorithmThe SA algorithm is an intelligent algorithm used to find the global optimal solution in the given search space. The algorithm arises from the idea of the thermo-mechanical annealing process: heating the material and then cooling it at a specific rate, so that the atoms in the material leave the position where the internal energy is locally minimized and reach the lower position than the original to increase the size of the grain and reduce the defects in the lattice.
In the algorithm, the point in the search space is regarded as the atom in the material and the solution of the point is regarded as the energy of the atom. At the beginning of the "high temperature", the probability that the points move randomly is higher and the points are easier to jump out of the local optimum. And then with the process of gradual "cooling", the points are gradually close to the global optimum, the probability of random movement is getting lower and lower. Finally, when the temperature reaches a proper threshold the global optimal value is found.
In order to further improve the efficiency of finding the optimal solution, we adopt a more detailed adaptation strategy to the original SA algorithm for the update of annealing temperature, so that the annealing temperature can only be updated until the new optimal value is found or at the end of the inner loop. And the amplitude of the update is increased with the current cycle time.
In the pseudo code, Δx is the parameter error, which responds to p' in Eq.6. f(x) is the objective function value, which responds to J(p') in Eq.5. When J(p') is maximum, the corresponding p' is optimal parameter error, i.e. CNOP-P. The pseudo code is as follows:
Pseudo Code: SA algorithm
Objective: min (or max) f(x), x=(x1, x2, x3, ∙∙∙, xn),
Input: initial particle position x0, initial temperature T0, number of external iteration Iter0, number of internal iteration Iteri
Process:
Set current particle position xc to x0, the current temperature T to T0
Calculate the value of current energy f(xc)
Set the best particle position xb to xc, the value of best energy f(xb) to f(xc)
for io=1:Itero
for ii=1: Iteri
Generate displacement Δx, make the new particle position xn=xc+Δx
Calculate the value of energy in new position f(xn)
Calculate the value of energy changed ΔE=f(xn)–f(xc)
if (ΔE < 0 & & f(xn) accord with norms) then
Set the best particle position xb to xn, the value of best energy f(xb) to f(xn)
Set the current particle position xc to xn, the value of current energy f(xc) to f(xn)
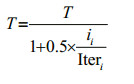
else
Generate a random rand
if 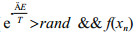
then
Set the current particle position xc to xn, the value of current energy f(xc) to f(xn)
end if
end if
end for
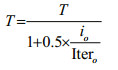
end for
3 RESULT AND DISCUSSION 3.1 OverviewFor studying the influence of three parameters, WD, VC and RDRG, on double gyre simulation, we firstly analyze parameters sensitivity by investigating how the uncertainty of parameters influences on the uncertainty of model prediction by solving CNOP-P with SA algorithm in ROMS. Then we verify whether the prediction error can be reduced by reducing the uncertainty of parameters.
The experimental process is as follows: The first step is to find the non-period oscillation of energy transition for double-gyre variation by adjusting parameters, then to select two transition period from the found non-period oscillation, one is from high energy to low energy called the first transition period and another is from low energy to high energy called the second transition period. The second and third steps are to carry out the corresponding parameters sensitivity experiments on the first and the second transition periods. The last step is to investigate how the decrease of uncertainty of sensitivity parameters, which is obtained in previous two steps, influences the prediction error of the double-gyre variation.
3.2 Selection for non-period oscillation and transition periodThe transition period is the stage where change is the most violent in the atmospheric and oceanic phenomena, and it is also the most concerned stage in the prediction. In order to observe the influence of the uncertainty of parameters on the transition period of the double gyre variation, the non-period oscillation of energy transition of the double-gyre variation is found firstly by adjusting parameters, and then we intercept a section from high energy to low energy and a section from low energy to high energy to carry out the subsequent studies.
When parameters are set to WD=-0.05 N/m2, VC=860 m2/s, RDRG=8×10-7 m/s, the double gyre in the region Λ shows a steady state. In our experiment, we separately change the value of one parameter while keeping other parameters unchanged to observe the influence of the three parameters on the energy transition. Among them, the values of WD are -0.06 N/m2, -0.07 N/m2, -0.09 N/m2, the values of VC are 688 m2/s, 602 m2/s, 516 m2/s, the values of RDRG are 8×10-13 m/s, 8×10-7 m/s25. Figure 1 shows the time series of the kinetic energy within 0–8 000 days in the region Λ under these value conditions.

|
| Fig.1 Time series of the kinetic energy with different parameter conditions |
It can be seen from Fig. 1 that when the value of WD is -0.09 N/m2, whose change percentage is 80% of the value of WD in the steady-state, or the value of VC is 516 m2/s, whose change percentage is 40% of the value of VC in the steady-state, the obvious nonperiod oscillation can be both obtained. However, the influence of RDRG on the time series of the kinetic energy is very small in any case. In order to ensure that the influences of reference parameters on the selected non-period oscillation are similar, we finally set the three parameters to WD=-0.07 N/m2, VC=602 m2/s, RDRG=8×10-7 m/s, where the percentage of WD changed is 40% of the value of WD in the steady-state, the percentage of VC changed is 30% of the value of VC in the steady-state and RDRG is the value of RDRG in the steady-state. The reason to choose these reference parameters is that RDRG has a little effect on the time series of the kinetic energy and the time series of the kinetic energy generated by WD alone or VC alone are similar under this condition. And time series of the kinetic energy of the non-period oscillation under this condition is shown in Fig. 2.

|
| Fig.2 Time series of the kinetic energy of the non-period oscillation WD=-0.07 N/m2, VC=602 m2/s, RDRG=8×10-7 m/s. |
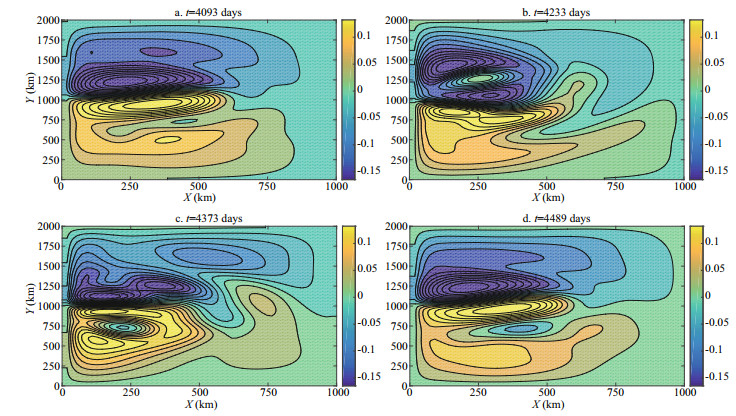
From Fig. 2, we can see time series of the kinetic energy when the three parameters are set to WD= -0.07 N/m2, VC=602 m2/s, RDRG=8×10-7 m/s, which are parameter values for the reference state in the experiment below. And then we select a section from high energy to low energy as the first transition period (TP1), whose optimization times is from 4 093 day to 4 233 day, totally 140 days, and a section from low energy to high energy as the second transition period (TP2), whose optimization times is from 4 373 day to 4 489 day, totally 116 days. TP1 and TP2 are shown as the red line and blue line in Fig. 2. The contour plots of sea surface height for these two transition periods' start-stop states are in Fig. 3. In the next experiment, we will carry out the study on parameters sensitivity on these two sections.
|
| Fig.3 Contour plots of sea surface height for start-stop states of TP1 and TP2 |
To avoid ignoring the interaction of parameters, we carry out the single parameter sensitivity experiment and the multiple parameters sensitivity experiment which deals with combination of two or three parameters.
In this subsection, when the parameter value is the reference parameter value, the propagator function value is 4.151×1012 m3/s2.We use the SA algorithm to solve the maximum objective function value whose parameter perturbation responds to CNOP-P, and then we analyze the sensitivity of parameters based on these results.
The constraint of the parameter is set to the absolute value of each parameter's perturbation, expressed as //ΔWD//≤σ1, //ΔVC//≤σ2, ∙∙∙, //ΔRDRG//≤σm.
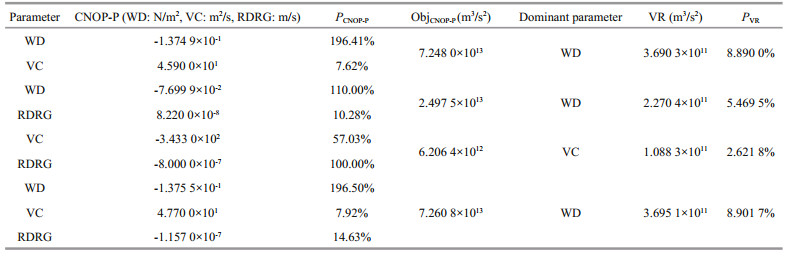
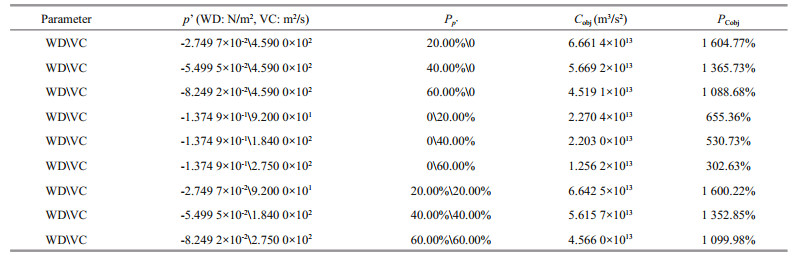
The analysis indices are listed in Table 1. Where CNOP-P is the optimal parameter error obtained from the experiment, J(p') is the objective function value when the parameter error is p', Mt(p) is the propagator function value when the parameter value is p and Mt (p) is calculated as the objective function whose reference state is initial state of the model, pr is the parameter value for the reference state. Dominant parameter is the parameter which the objective function value is mainly influenced by. Dominant parameter is the tested parameter in the single parameter sensitivity experiment.
For the single parameter sensitivity experiment of WD, VC and RDRG, the objective function value increases as the constraint value increases until the constraint σ1, σ2, σ2 are set to 7.667 7×10-2 N/m2, VC=3.458 0×102 m2/s, RDRG=8.000 0×10-7 m/s respectively. Here we get the global CNOP-P which is on the boundary of constraint. The constraint values in the single parameter sensitivity experiment of TP1 are shown in Table 2. The experiment results of CNOP-P and the indices value listed in Table 1 are shown in Table 3.

|
It can be seen that the corresponding constraint is different for every parameter. It is reasonable because every parameter has the different sensitivity which causes different influence on prediction.
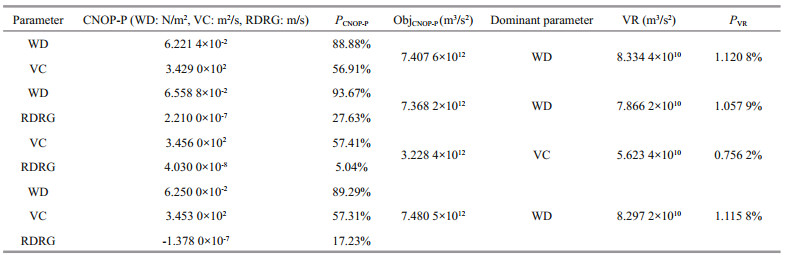
For the multiple parameters sensitivity experiment of WD, VC and RDRG, we also get the global CNOP-P for the four cases of parameters combination. We take the maximum value of the absolute value of WD, VC and RDRG in the four cases as their constraint, respectively 1.375 5×10-1 N/m2, VC=3.433 0×102 m2/s, RDRG=8.000 0×10-7 m/s, showed in Table 4. CNOP-P and the indices value listed in Table 1 are shown in Table 5. It can be seen that the optimal parameter error of every parameter for the four cases is different. Compared to Table 3, the optimal parameter error for multiple parameters is different from that for single parameter, which indicates interaction among multiple parameters.

|
From the experiment of this stage, we can see that, in the single parameter experiment, WD has the greatest influence on the objective function, the influence of VC is slightly weaker than that of WD, and the influence of RDRG is much weaker than that of WD and VC. In the multiple parameters experiment, when the combinations of parameters involve the perturbation of WD, WD is often the dominant parameter of the objective function value perturbation. From these we can see that the sensitivity sequence of these three parameters is WD>VC>>RDRG. At the same time, we can see that the parameter combination can often generate greater effect than single parameter, and if these parameters are sensitive parameters, the influence caused by them is often greater than the linear superposition of the influence caused by them separately such as the combination of WD and VC. We can also find that the change direction of nondominant parameter in the multiple parameters experiment is not necessarily same as that of the single parameter experiment, for example, the change value of VC causing the uncertainty in the single parameter sensitivity experiment is negative, however, it is positive when VC is the non-dominant parameter in the multiple parameters experiment of WD and VC.
3.4 Experiment of TP2In the experiment of this stage, we also conduct the single parameter sensitivity experiment and the multiple parameters sensitivity experiment for the same reason in Section 3.3.
In this stage, when the parameter value is the reference parameter value, the propagator function value is 7.436×1012 m3/s2. We use the method similar to that in Section 3.3 to obtain the CNOP-P, and then we verify results and further analyze the sensitivity of the parameters.
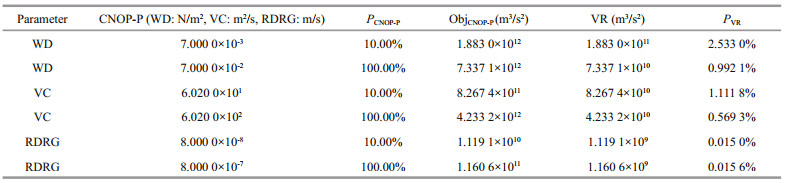
In the single parameter experiment of this stage, we find that no matter how we set the constraint boundary, the CNOP-P always lies on constraint boundary. Therefore, the local CNOP-Ps for the constraint boundaries which are 10% and 100% of the reference parameter value are selected to study the parameter sensitivity. The constraint values in the single parameter sensitivity experiment of TP2 are shown in Table 6. The experiment results of CNOP-P and the indices value listed in Table 1 are shown in Table 7.
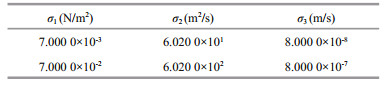
|
In the multiple parameter sensitivity experiment of this stage, the CNOP-P also always lies on constraint boundary. In order to ensure that parameters can have enough change range, the constraints in the multiple parameters sensitivity experiment of TP2 are set to the percentage of the parameter in the single parameter experiment of TP1 (Table 2). The experiment results of CNOP-P and the indices value listed in Table 1 are shown in Table 8.
From the experiment of this stage, from VR in the single parameter sensitivity experiment and the ratio of the dominant parameter in the multiple parameters experiment, we further confirm the result that the sensitivity sequence of these three parameters is WD>VC>>RDRG. At the same time, we also find that with the increase of WD and VC, their influence relatively reduces, while the influence of RDRG is almost unchanged, which can be seen from PVR in the single parameter experiment.
3.5 Experiment of prediction improvementThe above experiments show that WD and VC are relatively sensitive parameters. In addition, the CNOP-P obtained from TP1 is global CNOP-P, the CNOP-P obtained from TP2 is local CNOP-P. The global CNOP-P will cause the largest uncertainty for prediction, reducing parameter perturbation based on global CNOP-P will lead to the largest improvement for prediction. Therefore, in order to verify whether the prediction error can be reduced by reducing the uncertainty of WD and VC, we design prediction improvement experiment for TP1.
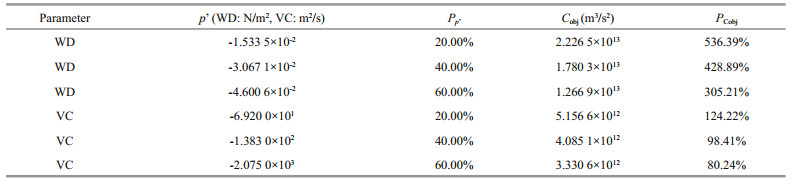
We firstly perform the experiment for the single parameter, then for two parameters by reducing the error of every sensitive parameter or their combination to 20%, 40%, and 60%. Table 9 are related evaluating indices. The result for the single parameter is shown in Table 10, and the result for two parameters is shown in Table 11.
where P' is the parameter error, CNOP-P is the optimal parameter error which is obtained from the experiment, J(p') is the objective function value when the parameter error is p', Mt(p) is the propagator function value when the parameter value is p, pr is the parameter value for the reference state.
From the table, we can find that the objective function value decreases 3–16 times relative to the objective function value for reference state after reducing the error of sensitive parameters. The table indicates that the decrease of the uncertainty of sensitivity parameters can effectively reduce the prediction error of the double gyre variation.
4 CONCLUSIONIn this paper, we study the sensitivity of the single parameter and the combination of multiple parameters based on CNOP-P method, for WD, VC and RDRG these three parameters in double-gyre variation simulation of ROMS. We also propose an improved SA algorithm to solve CNOP-P. In the experiment, we firstly find the non-period oscillation of kinetic energy time series of double gyre variation, then extract two transition periods, which are respectively from high energy to low energy and from low energy to high energy. For every transition period, we apply SA algorithm to finding proper constraint and solving CNOP-P of the single parameter and the combination of multiple parameters to study the parameters sensitivity. Experiments results show that proposed improved SA algorithm is an effective method to solve CNOP-P. For the single parameter, when simulating double gyre variation in ROMS, we find that WD can cause the greatest influence, VC has the slightly weaker influence than WD, and the influence of RDRG is far less than them, that is, WD>VC>>RDRG. Meanwhile for the sensitive WD and VC, the greater their values are, the smaller the magnitude of their influence is; for the insensitive RDRG, the influence is almost no change. For the combination of multiple parameters, WD always has dominant effect, RDRG does not take the role of the dominant parameter in any combination, which further confirms that the sensitive sequence is WD>VC>>RDRG. In addition, we find that the uncertainty of the model result caused from the error of the combination is larger than that of the single parameter. For the combinations of sensitive parameters, their influence is often greater than the linear superposition of their separate influence. After determining that WD and VC are sensitive parameters, by reducing error of WD and VC on basis of the optimal parameters error, we analysis how the sensitive parameters and their combination effect on the simulation of double gyre variation. Through the experiment, we verify the effect of reducing the error of sensitive parameters on reducing the uncertainty of model simulation, which confirm the value of the research of parameters sensitivity.
The result in this paper will be more persuasive if using observation data, and we only study the WD, VC and RDRG three parameters. In the future, we will study the sensitivity of more parameters for the current in ROMS with observation data.
5 DATA AVAILABILITY STATEMENTThe data supporting the conclusions of this study are included in this article.
6 ACKNOWLEDHMENTThe authors would like to thank WANG Qiang at the Institute of Oceanology, Chinese Academy of Sciences, for useful supports with the guidance of CNOP-P and the simulation of double gyre, and other members of our research group for helpful and valuable suggestions.
Haidvogel D B, Arango H G, Hedstrom K, Beckmann A, Malanotte-Rizzoli P, Shchepetkin A F. 2000. Model evaluation experiments in the North Atlantic Basin:simulations in nonlinear terrain-following coordinates. Dynamics of Atmospheres and Oceans, 32(3-4): 239-281.
DOI:10.1016/S0377-0265(00)00049-X |
Hall M C G, Cacuci D G, Schlesinger M E. 1982. Sensitivity analysis of a radiative-convective model by the adjoint method. Journal of Atmospheric Sciences, 39(9): 2038-2050.
DOI:10.1175/1520-0469(1982)039<2038:SAOARC>2.0.CO;2 |
Hamby D M. 1994. A review of techniques for parameter sensitivity analysis of environmental models. Environmental Monitoring and Assessment, 32(2): 135-154.
DOI:10.1007/BF00547132 |
Jiang S, Jin F F, Ghil M. 1995. Multiple equilibria, periodic, and aperiodic solutions in a wind-driven, double-gyre, shallow-water model. Journal of Physical Oceanography, 25(5): 764-786.
DOI:10.1175/1520-0485(1995)025<0764:MEPAAS>2.0.CO;2 |
Kirkpatrick S, Gelatt C D Jr, Vecchi M P. 1983. Optimization by simulated annealing. Science, 220(4598): 671-680.
DOI:10.1126/science.220.4598.671 |
Lu J X, Hsieh W W. 1997. Adjoint data assimilation in coupled atmosphere-ocean models:Determining model parameters in a simple equatorial model. Quarterly Journal of the Royal Meteorological Society, 123(543): 2115-2139.
DOI:10.1002/(ISSN)1477-870X |
Lu J X, Hsieh W W. 1998. On determining initial conditions and parameters in a simple coupled atmosphere-ocean model by adjoint data assimilation. Tellus A:Dynamic Meteorology and Oceanography, 50(4): 534-544.
DOI:10.3402/tellusa.v50i4.14531 |
Mahadevan A, Lu J, Meacham S P, Malanotte-Rizzoli P. 2001. The predictability of large-scale wind-driven flows. Nonlinear Processes in Geophysics, 8(6): 449-465.
DOI:10.5194/npg-8-449-2001 |
Marchesiello P, McWilliams J C, Shchepetkin A. 2003. Equilibrium structure and dynamics of the California Current System. Journal of Physical Oceanography, 33(4): 753-783.
DOI:10.1175/1520-0485(2003)33<753:ESADOT>2.0.CO;2 |
Moore A M, Arango H G, Di Lorenzo E, Cornuelle B D, Miller A J, Neilson D J. 2004. A comprehensive ocean prediction and analysis system based on the tangent linear and adjoint of a regional ocean model. Ocean Modelling, 7(1): 227-258.
|
Moore A M. 1999. Wind-induced variability of ocean gyres. Dynamics of Atmospheres and Oceans, 29(2-4): 335-364.
DOI:10.1016/S0377-0265(99)00010-X |
Mu M, Duan W S, Wang B. 2003. Conditional nonlinear optimal perturbation and its applications. Nonlinear Processes in Geophysics, 10(6): 493-501.
DOI:10.5194/npg-10-493-2003 |
Mu M, Duan W, Wang Q, Zhang R. 2010. An extension of conditional nonlinear optimal perturbation approach and its applications. Nonlinear Processes in Geophysics, 17(2): 211-220.
DOI:10.5194/npg-17-211-2010 |
Nauw J J, Dijkstra H A, Chassignet E P. 2004. Frictionally induced asymmetries in wind-driven flows. Journal of Physical Oceanography, 34(9): 2057-2072.
DOI:10.1175/1520-0485(2004)034<2057:FIAIWF>2.0.CO;2 |
Nauw J J, Dijkstra H A. 2001. The origin of low-frequency variability of double-gyre wind-driven flows. Journal of Marine Research, 59(4): 567-597.
DOI:10.1357/002224001762842190 |
Navon I M. 1998. Practical and theoretical aspects of adjoint parameter estimation and identifiability in meteorology and oceanography. Dynamics of Atmospheres and Oceans, 27(1-4): 55-79.
DOI:10.1016/S0377-0265(97)00032-8 |
Pierini S. 2010. Coherence resonance in a double-gyre model of the Kuroshio Extension. Journal of Physical Oceanography, 40(1): 238-248.
DOI:10.1175/2009JPO4229.1 |
Primeau F, Newman D. 2008. Elongation and contraction of the western boundary current extension in a shallowwater model:A bifurcation analysis. Journal of Physical Oceanography, 38(7): 1469-1485.
DOI:10.1175/2007JPO3658.1 |
Primeau F. 2002. Multiple equilibria and low-frequency variability of the wind-driven ocean circulation. Journal of Physical Oceanography, 32(8): 2236-2256.
DOI:10.1175/1520-0485(2002)032<2236:MEALFV>2.0.CO;2 |
Ren J H, Yuan S J, Mu B. 2016. Parallel modified artificial bee colony algorithm for solving conditional nonlinear optimal perturbation In: 2016 IEEE 18th International Conference on High Performance Computing and Communications; IEEE 14th International Conference on Smart City; IEEE 2nd International Conference on Data Science and Systems (HPCC/SmartCity/DSS), IEEE, Sydney, NSW, Australia. p.333-340.
|
Sapsis T P, Dijkstra H A. 2013. Interaction of additive noise and nonlinear dynamics in the double-gyre wind-driven ocean circulation. Journal of Physical Oceanography, 43(2): 366-381.
DOI:10.1175/JPO-D-12-047.1 |
Shchepetkin A F, Mcwilliams J C. 2003. A method for computing horizontal pressure-gradient force in an oceanic model with a nonaligned vertical coordinate. Journal of Geophysical Research:Oceans, 108(C3): 3090.
DOI:10.1029/2001JC001047 |
Shchepetkin A F, Mcwilliams J C. 2005. The regional oceanic modeling system (ROMS):a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Modelling, 9(4): 347-404.
DOI:10.1016/j.ocemod.2004.08.002 |
Shen J, Medjo T T, Wang S. 1999. On a wind-driven, doublegyre, quasi-geostrophic ocean model:numerical simulations and structural analysis. Journal of Computational Physics, 155(2): 387-409.
DOI:10.1006/jcph.1999.6344 |
Simonnet E, Ghil M, Dijkstra H. 2005. Homoclinic bifurcations in the quasi-geostrophic double-gyre circulation. Journal of Marine Research, 63(5): 931-956.
DOI:10.1357/002224005774464210 |
Sun G D, Mu M. 2017. A new approach to identify the sensitivity and importance of physical parameters combination within numerical models using the LundPotsdam-Jena (LPJ) model as an example. Theoretical and Applied Climatology, 128(3-4): 587-601.
DOI:10.1007/s00704-015-1690-9 |
Sura P, Penland C. 2002. Sensitivity of a double-gyre ocean model to details of stochastic forcing. Ocean Modelling, 4(3-4): 327-345.
DOI:10.1016/S1463-5003(02)00008-2 |
Van Scheltinga A D T, Dijkstra H A. 2008. Conditional nonlinear optimal perturbations of the double-gyre ocean circulation. Nonlinear Processes in Geophysics, 15(5): 727-734.
DOI:10.5194/npg-15-727-2008 |
Wen S, Yuan S, Mu B, et al. 2015. PCGD:Principal components-based great deluge method for solving CNOP. IEEE Congress on Evolutionary Computation, (CEC): 1513-1520.
|
White M A, Thornton P E, Running S W, et al. 2000. Parameterization and sensitivity analysis of the BIOMEBGC terrestrial ecosystem model:net primary production controls. Earth Interactions, 4(3): 1-85.
DOI:10.1175/1087-3562(2000)004<0003:PASAOT>2.0.CO;2 |
Wilkin J L, Arango H G, Haidvogel D B, et al. 2005. A regional ocean modeling system for the Long-term Ecosystem Observatory. Journal of Geophysical Research:Oceans, 110(C6): C06S91.
|
Yin X D, Wang B, Liu J J, et al. 2014. Evaluation of conditional non-linear optimal perturbation obtained by an ensemblebased approach using the Lorenz-63 model. Tellus Series A:Dynamic Meteorology & Oceanography, 66(2): 116-118.
|
Yuan S J, Li M, Mu B, et al. 2016. PCAFP for solving CNOP in double-gyre variation and its parallelization on clusters.In: 2016 IEEE 18th International Conference on High Performance Computing and Communications, Sydney, NSW, Australia. p.284-291.
|
Yuan S J, Yan J H, Mu B et al. 2015b. Parallel dynamic step size sphere-gap transferring algorithm for solving conditional nonlinear optimal perturbation.: 2015 17th, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, and 2015 IEEE 12th International Conference on Embedded Software and Systems. IEEE, New York, NY, USA. p.559-565.
|
Yuan S, Qian Y, Mu B. 2015a. Paralleled continuous Tabu search algorithm with sine maps and staged strategy for solving CNOP. In: Wang G, Zomaya A, Martinez G et al.eds. Springer, Cham.
|
Zaehle S, Sitch S, Smith B, et al. 2005. Effects of parameter uncertainties on the modeling of terrestrial biosphere dynamics. Global Biogeochemical Cycles, 19(3): GB3020.
|
Zhang K, Mu M, Wang Q. 2015. The impact of initial error on predictability of Double-gyre variability. Marine Science, 39(5): 120-128.
(in Chinese) |
Zhang L L, Yuan S J, Mu B, et al. 2017. CNOP-based sensitive areas identification for tropical cyclone adaptive observations with PCAGA method. Asia-Pacific Journal of Atmospheric Sciences, 53(1): 63-73.
DOI:10.1007/s13143-017-0005-8 |
 2019, Vol. 37
2019, Vol. 37