Institute of Oceanology, Chinese Academy of Sciences
Article Information
- YANG Yongzeng, SHI Yongfang, YU Chencheng, TENG Yong, SUN Meng
- Study on surface wave-induced mixing of transport flux residue under typhoon conditions
- Journal of Oceanology and Limnology, 37(6): 1837-1845
- http://dx.doi.org/10.1007/s00343-019-8268-9
Article History
- Received Sep. 26, 2018
- accepted in principle Dec. 4, 2018
- accepted for publication May. 10, 2019
2 Laboratory for Regional Oceanography and Numerical Modeling, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266061, China;
3 Key Laboratory of Marine Science and Numerical Modeling, Ministry of Natural Resources, Qingdao 266061, China;
4 Zhejiang University, Zhoushan 316021, China
Interactions among various ocean motions and their physical-mathematical descriptions are the main objectives of the ocean dynamic system. Ocean mixing and its reasonable parameterization are of significant importance for modeling of the ocean circulation at large scale. For the formation of the upper mixed layer, surface wave-induced mixing plays an important role. It consists of three mechanisms: the first is the mixing process induced by surface wave-generated turbulence (Yuan et al., 1999, 2013). Based on the equilibrium solution of the second-order turbulence closure model under assumption of high certainty, the analytical wave-induced mixing parameter was proposed and validated by field observations of the dissipation rate. Babanin (2006), Dai et al. (2010) tested and confirmed the wave-generated turbulence through mechanically generated laboratory wave experiments. Babanin and Chalikov (2012) also presented that the vorticity and turbulence usually occur in vicinity of wave crests and then spread over upwind slope and downward through a numerical wave-turbulence model. Yang et al.(2003, 2004) estimated the amplitude of analytical wave-induced vertical mixing parameter Bv in China Seas by using the LAboratory of Geophysical Fluid Dynamics, WAve Model (LAGFD-WAM), the mixing strength is significant and play an important role in the upper layer. Qiao et al.(2004, 2008, 2010), Xia et al.(2004, 2006) developed the MASNUM (Key Laboratory of MArine Science and NUmerical Modeling) wave-tide-circulation coupled model in the global oceans to improve the upper mixed layer simulation.
The second is the effect of breaking waves on ocean surface temperature and surface boundary layer deepening. Since wave breaking can produce downward energy flux and create a nonzero length scale to the surface boundary conditions of the turbulence closure model, it can enhance mixing in surface layer by turbulence (Agrawal et al., 1992; Craig and Banner, 1994; Terray et al., 1996, 1997, 2000). Sun et al. (2006) studied the local equilibrium between diffusion and dissipation of the turbulence kinetic energy (TKE) in the presence of wave breaking. The turbulent energy dissipated in the wave-enhanced layer would increase by one time as compared with the results under zero wave breaking. And a new local equilibrium between diffusion and dissipation of TKE was reached, which had a good agreement with some measurements.
The third is the mixing process induced by the wave transport residue near strong currents, in which the background velocity, density, temperature and salinity shear is apparently distinct. Hasselmann (1970), Xu and Bowen (1994), Sun et al.(2003, 2006) studied the wave-driven effect of Coriolis-Stokes force on large-scale motions. In conditions of high sea state, their comparison results indicate that the Coriolis-Stokes stress plays an important role in global and regional oceans. Lewis and Belcher (2004) and Polton et al. (2005) also analyzed its effect on vertical ocean Ekman structure. In conditions of even modest sea state, they concluded that the CoriolisStokes forcing can be a considerable fraction of the depth-integrated wind-driven transport and change the current profile through all depths. Yang et al. (2009) proposed a mixing model for the residue of wave-turbulence interaction to circulation through the Reynolds average upon characteristic wave length scale, but the linearized decomposition coefficients were undetermined yet. Zhang et al. (2015) performed numerical experiments near the Kuroshio to analyze the improvements of temperature by the wave transport flux residual. Shi et al. (2016) set up several experiments based on the Regional Ocean Model System (ROMS) to assess the effects of the mixing of wave transport flux residue on monthly mean sea surface temperature (SST) and mixed layer depth (MLD) in summer. The overestimated SST and underestimated MLD in control experiment is remarkably improved and more comparable to Levitus data especially in the strong current regions. In the previous studies stated above, the mixing effect on density, temperature and salinity induced by the wave transport residue was considered coarsely. A relatively comprehensive and simplified exposition of the wave transport flux residue should be proposed inextenso, and its mixing mechanism should be discussed further especially under typhoon conditions with strong background current.
This paper is organized as follows. A more reasonable decomposition scheme is proposed and a model for the wave transport flux residue is presented in detail in Section 2. In Section 3, under simple-harmonic wave conditions, we design tentative experiments to estimate the effect of the wave transport flux residue under typhoon conditions. Conclusions are summarized in Section 4.
2 MODEL DERIVATION 2.1 Decomposition schemeIn the usual notation, let (xi, i=1, 2, 3) be rectangular co-ordinates. Let (u′SMi, i=1, 2, 3) denote the wave velocities; T′SM, s′SM, p′SM, ρ′SM, the perturbations of temperature, salinity, pressure and density induced by ocean waves. For further interpretation of wavecurrent interaction, more comprehensive governing equations for wave motion should be considered, which can be seen in Yuan et al. (2012):
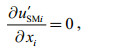 (1)
(1)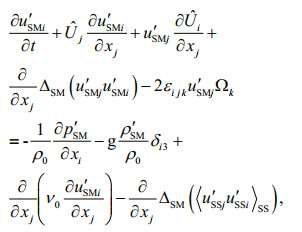 (2)
(2)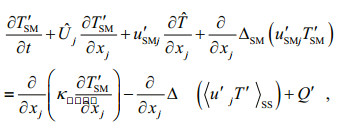 (3)
(3) (4)
(4)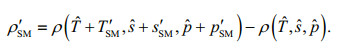 (5)
(5)where 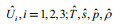
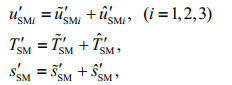 (6)
(6)where 


 (7)
(7)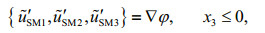 (8)
(8)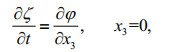 (9)
(9)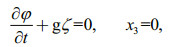 (10)
(10)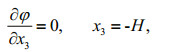 (11)
(11)where φ is velocity potential, ζ the elevation of waves, and H the water depth. The solutions of above equations are given by
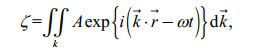 (12)
(12)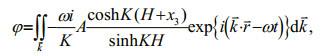 (13)
(13)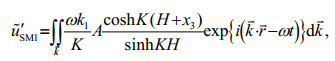 (14)
(14) (15)
(15)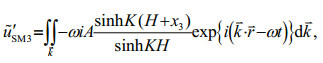 (16)
(16)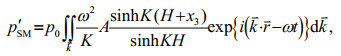 (17)
(17) (18)
(18)where 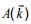

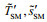
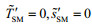
For the perturbations 
 (19)
(19)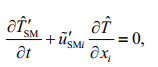 (20)
(20)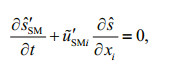 (21)
(21)The advection terms 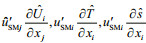

 (22)
(22)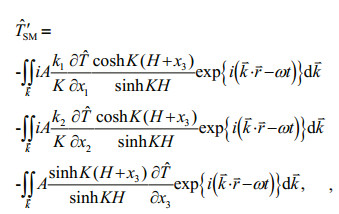 (23)
(23) (24)
(24)These approximate solutions clearly show the dependence linearly on the background current shear, and explicate the wave-current interactions despite a relative simplified approximation used here. By taking into account the given solutions (Eqs.14–18 and Eqs.22–24), we can derive directly the wave transport residue below to interpret its mixing effects.
2.2 Mixing modelThe effect of small scale motions on large ones can induce two facts, one is stratification and the other is uniformity appeared in physical phenomena. Both sorts of effect were discussed in many papers and summed up to mixing effect in Yuan et al. (2012), where they proposed it as transport flux residue derived from decomposition and Reynolds average of nonlinear advection terms. Here we also call the transport flux residue as mixing process, but it may play positive or negative role for physical mixing. That is to say, the transport flux residue may stratify or uniform the ocean horizontally or vertically. Phillips (1977), Yuan et al. (1991) derived the wave energy balance equation incorporating the energy transfer from background current to waves through wave radiation stress, but how its reaction to the current profile and mixing to the upper layer are still lack and need to investigate further. In addition, it is inappropriate that they assumed background current to be steady and vertically identical especially under typhoon conditions. Corresponding to Eq.6, the ocean mixings of momentum, temperature and salinity of surface waves to circulation can be expressed as
 (25)
(25)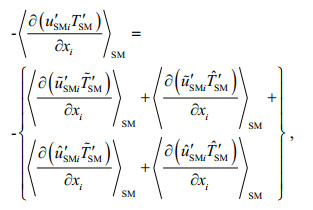 (26)
(26)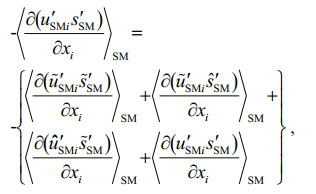 (27)
(27)where < >SM denotes the Reynolds average in wave motion. The first term in the right hand of Eq.25 is related to the so-called radiation stress introduced by Longuet-Higgins and Stewart(1962, 1964), which was approximated through second order and widely used for wave-induced flow in shallow water. The second terms in the right hand of Eqs.25–27 are the major mixing processes. Noting that the continuity equation for 
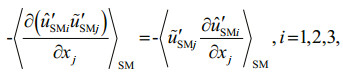 (28)
(28)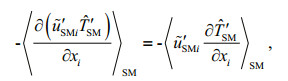 (29)
(29)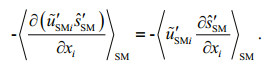 (30)
(30)Under typhoon conditions, the wave energy spectrum width is narrow, so the vertical mixing term in Eq.28 can be expressed as Fourier integrals:
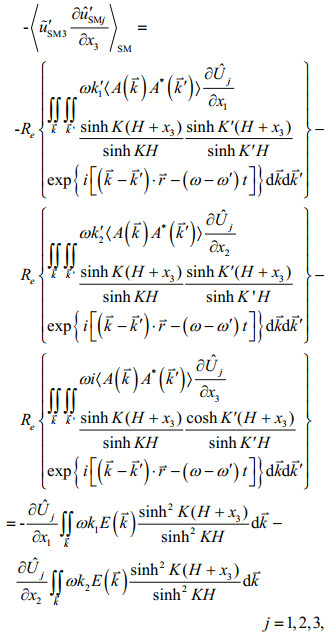 (31)
(31)provided that the hyperbolic function in the last two terms varies slowly in comparison with the wave energy spectrum. Such expression averaged in wave motion is more practical for our following numerical experiments. Correspondingly,
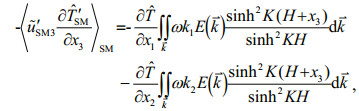 (32)
(32)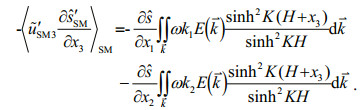 (33)
(33)The horizontal mixing terms in Eqs.28, 29, 30 can also be accordingly derived as above. After sum-up respectively, the mixing model for momentum, temperature and salinity of surface waves to circulation is given by
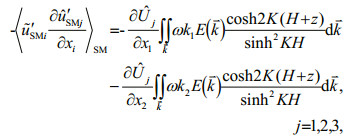 (34)
(34)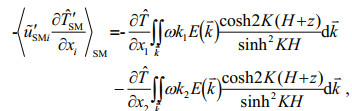 (35)
(35)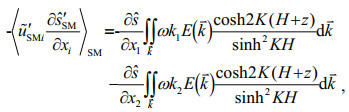 (36)
(36)in which the modulation of background current shear instability generation to surface waves is reserved apparently in our first order approximation scheme. This indicates that the model has the ability to implicate the effect of wave transport flux residue on mixing, especially under typhoon conditions with strong background current.
3 NUMERICAL EXPERIMENTHere we only analyze the effect of wave transport flux residue on temperature under simple-harmonic wave conditions, thus the dominant gravitational wave solutions can be written as
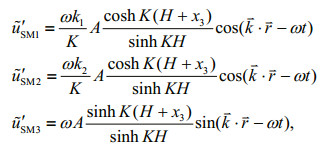
and the perturbation solutions generated by the background current shear can be written as
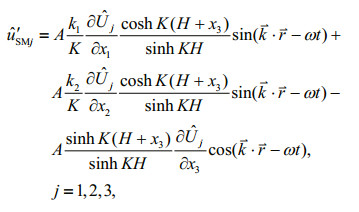

Hence,
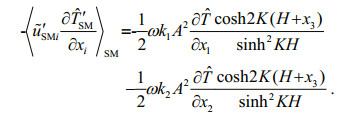 (37)
(37)For deep water, it is easily expressed as
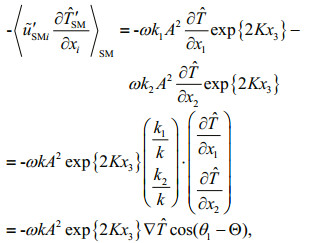 (38)
(38)where θ1, Θ are the directions of wave-number and the gradient of water temperature, which are depicted along the transect of tropic cyclone (Fig. 1). Here we suppose the direction of the gradient of water temperature is simply perpendicular to the path of tropic cyclone, because a large cooling area remained after the tropic cyclone past, especially a much cooling belt existed along the path of cyclone. In Fig. 2, when typhoon Matsa passed across the east of Taiwan, China, TMI (TRMM Microwave Imager) at TRMM satellite observed the cooling down of SST (Aug 4, 2005), the SST reduced from 29℃ to 26.4℃ and recovered to 27.8℃ after typhoon passed (Shao et al., 2015). There are many studies to interpret the dynamic cooling mechanism (Lai et al., 2013; Liu et al., 2007, 2014; Wang and Qiao, 2008), especially the wave-generated turbulence mixing plays an important role for the formation of upper mixed layer.

|
| Fig.1 Sketch of directions along the transect of cyclone |

|
| Fig.2 Typhoon Matsa induced cooling of SST observed by TRMM satellite in the east of Taiwan, China Black line AB represents the transect; circles represent the track of typhoon Matsa. |
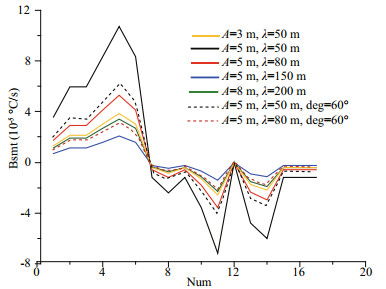
Here we estimate the decreasing rate of SST due to wave transport flux residue (Fig. 3). The horizontal axis represents the serial points along a typical transect across the cooling belt in Fig. 2 from southwest to northeast. A is the amplitude, and λ is the wave length. Solid lines are the values of wave transport flux residue with the degree θ1–Θ=30° or 150°, while the dashed lines are θ1–Θ=60° or 120°. The maximum value of the wave transport flux residue can reach up to (8–10)×10-5℃/s. In the right side of cyclone path, the dominant wave direction is consistent with the gradient of the SST (i.e. θ1–Θ < 90°), so the wave transport flux residue is negative from Eq.38 and plays a cooling role; while in the left side, the wave transport flux residue plays a heating role oppositely. This further intensifies the asymmetry of the cooling area of SST.
|
| Fig.3 The decreasing rate of SST due to wave transport flux residue |
From Eq.38 for deep water condition, the transport flux residue attenuates exponentially. Figure 4 shows the rapid attenuation with water depth, which is consistent with the exponent expression correspondingly. It attenuates slower for waves with longer wave length. Under typhoon conditions, it can affect 20–40 m layer with the dominant wave length of about 80 m.

|
| Fig.4 Attenuation of the transport flux residue with water depth |
How much of a role does the wave transport flux residue play in the upper layer? Here we define an analogue Reynolds Number for harmonic waves, i.e.
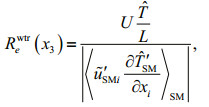 (39)
(39)where U, L are the horizontal velocity and spatial characteristic scale of background current. Here we let U=1.0 m/s, L=50.0 km for simplicity. As for wavegenerated turbulence mixing (Qiao et al., 2004; Xia et al., 2004; Yang et al., 2004; Yuan et al., 2013), its analogue Reynolds Number is defined as
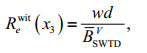 (40)
(40)where
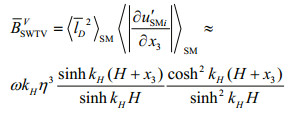
for harmonic waves, and BSWTVV≈ωkHA3 exp{3kHx3} in deep water conditions; w, d are the vertical velocity and characteristic scale, and let w=0.01 m/s, d=1.0 m here. Both dimensionless analogue Reynolds Numbers expose their mixing extent in comparison with advection terms.
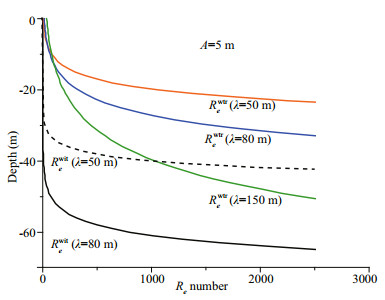
Figure 5 shows the comparison of analogue Reynolds Numbers between the wave transport flux residue and wave-generated turbulence mixing. Here we only set the wave amplitude to 5 m, but the wave length varies from 50 m, 80 m to 150 m. For Re=1 000, the influence of wave transport flux residue can reach up to 40 m depth with wavelength 150 m, which is equivalent to the wave-generated turbulence mixing with wavelength 50 m. Although the wave-generated turbulence mixing with longer wavelength can affected much deeper water, the wave transport flux residue plays an important role in 20–50 m depth and cannot be ignored consciously especially in typhoon conditions.
|
| Fig.5 Variation of analogue Reynolds numbers of the wave transport flux residue and wave-generated turbulence mixing with water depth |
It should be evaluated the influence on the coast area before typhoon landing, where the water is mixed identically from top to bottom due to huge waves and storm tide. Here Eq.37 is used for shallow water, and let U=2.0 m/s for storm current. Because of the varied topography, here we let w=0.5 m/s. Figure 6 shows the analogue Reynolds Numbers of the wave transport flux residue and wave-generated turbulence mixing where the water depth is 10 m. Both are comparable and much less than Re=2 000, where the wave amplitude is 2 m and the wavelength λ=30, 50 m. Zhou et al. (2012), Shao et al. (2015) investigated the sharp decreasing of phytoplankton chlorophyll-a (Chl-a) concentration in the nearshore area due to intense, fast moving typhoons. Both overwhelming dynamical mixing processes can remarkably change the coastal ecological environment, and should be two important causing disaster factors for further marine hazards assessment.

|
| Fig.6 Same as Fig. 5 but for shallow water depth |
The role of the surface wave-induced mixing of transport flux residue is studied tentatively under typhoon conditions. Based on the decomposition scheme for surface waves, we proposed an analytic model to describe the interactions between waves and the background current. Perturbations generated by the background current shear are derived, and the mixing terms of wave transport flux residue are expressed analytically as a function of wave-number spectrum for further application.
We roughly estimate the intensity of wave transport flux residue under typhoon conditions. under strong current conditions, it has the order of (8–10)×10-5℃/s at surface, attenuates exponentially with water depth, and can even affect 20–40 m layer with the dominant wave length of about 80 m. It plays an important role for the cooling feature observed by satellite remote sensing, and is consistent with the spatial cooling asymmetry. Here we suppose the water stratification is steady and uniform. But in the real ocean, the wave transport flux residue varies much temporally and spatially, mainly depends on the instability of the wind-driven current shear.
Analogue Reynolds Numbers are proposed for comparison between the wave-generated turbulence mixing and the wave transport flux residue. The influence of the latter can be comparable to the former under typhoon conditions, which cannot be ignored consciously especially in 20–50 m depth. Particularly in coastal areas, both analogue Reynolds Numbers are much less than Re=2 000, and remarkably change the coastal ecological environment. This indicates that a more comprehensive coupling model including these two dynamical mechanisms should be considered simultaneously, and their effectiveness needs to be studied successively in the future numerical experiments.
5 DATA AVAILABILITY STATEMENTThe datasets generated and/or analysed during the current study are available from the corresponding author on reasonable request.
Agrawal Y C, Terray E A, Donelan M A, Hwang P A, Williams Ⅲ A J, Drennan W M, Kahma K K, Krtaigorodskii S A. 1992. Enhanced dissipation of kinetic energy beneath surface waves. Nature, 359(6392): 219-220.
DOI:10.1038/359219a0 |
Babanin A V, Chalikov D. 2012. Numerical investigation of turbulence generation in non-breaking potential waves. J.Geophys. Res., 117(C11): C06010.
DOI:10.1029/2012JC007929 |
Babanin A V. 2006. On a wave-induced turbulence and a wavemixed upper ocean layer. Geophys. Res. Lett., 33(20): L20605.
DOI:10.1029/2006GL027308 |
Craig P D, Banner M L. 1994. Modeling wave-enhanced turbulence in the ocean surface layer. J. Phys. Oceanogr., 24(12): 2546-2559.
DOI:10.1175/1520-0485(1994)024<2546:MWETIT>2.0.CO;2 |
Dai D J, Qiao F L, Sulisz W, Han L, Babanin A. 2010. An experiment on the nonbreaking surface-wave-induced vertical mixing. J. Phys. Oceanogr., 40(9): 2180-2188.
DOI:10.1175/2010JPO4378.1 |
Hasselmann K. 1970. Wave-driven inertial oscillations. Geophys. Fluid Dyn., l(3-4): 463-502.
|
Lai Q Z, Ma L M, Huang W, Wu L G. 2013. The ocean response to Typhoon Morakot (2009) in the western North Pacific boundary region. Acta Oceanol. Sin., 35(3): 65-77.
(in Chinese with English abstract) |
Lewis D M, Belcher S E. 2004. Time-dependent, coupled, Ekman boundary layer solutions incorporating Stokes drift. Dyn. Atmos. Oceans, 37(4): 313-351.
|
Liu Z H, Xu J P, Sun C H, Wu X F. 2014. An upper ocean response to Typhoon Bolaven analyzed with Argo profiling floats. Acta Oceanol. Sin., 33(11): 90-101.
DOI:10.1007/s13131-014-0558-7 |
Liu Z H, Xu J P, Zhu B K, Sun C H, Zhang L F. 2007. The upper ocean response to tropical cyclones in the northwestern Pacific analyzed with Argo data. Chin. J.Oceanol. Limnol., 25(2): 123-131.
DOI:10.1007/s00343-007-0123-8 |
Longuet-Higgins M S, Stewart R W. 1962. Radiation stress and mass transport in gravity waves, with application to 'surf beats'. J. Fluid Mech., 13(4): 481-504.
DOI:10.1017/S0022112062000877 |
Longuet-Higgins M S, Stewart R W. 1964. Radiation stresses in water waves; a physical discussion, with applications. Deep Sea Res. Oceanogr. Abst., 11(4): 529-562.
DOI:10.1016/0011-7471(64)90001-4 |
Mei Q Z. 1984. Dynamics of Water Waves. Science Press, Beijing.
(in Chinese)
|
Phillips O M. 1977. The Dynamics of the Upper Ocean. 2nd edn. Cambridge University Press, Cambridge.
|
Polton J A, Lewis D M, Belcher S E. 2005. The role of waveinduced Coriolis-Stokes forcing on the wind-driven mixed layer. J. Phys. Oceanogr., 35(4): 444-457.
|
Qiao F L, Yang Y Z, Xia C S, Yuan Y L. 2008. The role of surface waves in the ocean mixed layer. Acta Oceanol.Sin., 27(3): 30-37.
|
Qiao F L, Yuan Y L, Ezer T, Xia C S, Yang Y Z, Lü X G, Song Z Y. 2010. A three-dimensional surface wave-ocean circulation coupled model and its initial testing. Ocean Dyn., 60(5): 1339-1355.
DOI:10.1007/s10236-010-0326-y |
Qiao F L, Yuan Y L, Yang Y Z, Zheng Q A, Xia C S, Ma J. 2004. Wave-induced mixing in the upper ocean:Distribution and application to a global ocean circulation model. Geophys. Res. Lett., 31(11): L11303.
DOI:10.1029/2004GL019824 |
Shao J C, Zhao H, Shen C Y, Lü J H. 2015. Influence of Typhoon Matsa on phytoplankton chlorophyll-a in the northwest Pacific Ocean offshore and alongshore. J.Guangdong Ocean Univ., 35(4): 67-74.
(in Chinese with English abstract) |
Shi Y F, Wu K J, Yang Y Z. 2016. Preliminary results of assessing the mixing of wave transport flux residual in the upper ocean with ROMS. J. Ocean Univ. China, 15(2): 193-200.
DOI:10.1007/s11802-016-2706-5 |
Sun F, Qian C, Wang W, et al. 2003. Wave-induced radiation stress and its driving effect on current. Sci. China, Ser. D, 33(8): 791-798.
(in Chinese) |
Sun F, Wei Y L, Wu K J. 2006a. Wave-induced radiation stress under geostrophic condition. Acta Oceanol. Sin., 28(6): 1-4.
(in Chinese with English abstract) |
Sun Q, Guan C L, Song J B. 2006b. Effect of wave breaking on turbulent energy budgets in ocean surface mixed layer. Oceanol. Limnol. Sin., 37(1): 69-74.
(in Chinese with English abstract) |
Terray E A, Donelan M A, Agrawal Y C, Drennan W M, Kahma K K, Williams A J, Hwang P A, Kitaigorodskii S A. 1996. Estimates of kinetic energy dissipation under breaking waves. J. Phys. Oceanogr., 26(5): 792-807.
DOI:10.1175/1520-0485(1996)026<0792:EOKEDU>2.0.CO;2 |
Terray E A, Donelan M A, Agrawal Y C, Drennan W M, Kahma K K, Williams Ⅲ A J, Hwang P A, Kitaigorodskii S A. 1997. Reply. J. Phys. Oceanogr., 27(10): 2308-2309.
DOI:10.1175/1520-0485(1997)027<2308:R>2.0.CO;2 |
Terray E A, Drennan W M, Donelan M A. 2000. The vertical structure of shear and dissipation in the ocean surface layer. In: Proceedings Symposium on the Wind-driven Air-Sea Interaction. ADFA Document Production Centre, Canberra, Australia. p.239-245.
|
Wang G S, Qiao F L. 2008. Ocean temperature responses to Typhoon Mstsa in the East China Sea. Acta Oceanol. Sin., 27(4): 26-38.
|
Wen S C, Yu Z W. 1984. Wave Theories and Calculation Principles. Science Press, Beijing.
(in Chinese)
|
Wu Y G, Tao M D. 2011. Fundamental Dynamics of Water Waves. Fudan University Press, Shanghai.
(in Chinese)
|
Xia C S, Qiao F L, Yang Y Z, Ma J, Yuan Y L. 2006. Threedimensional structure of the summertime circulation in the Yellow Sea from a wave-tide-circulation coupled model. J. Geophys. Res., 111(C11): C11S03.
DOI:10.1029/2005JC003218 |
Xia C S, Qiao F L, Zhang M N, Yang Y Z, Yuan Y L. 2004. Simulation of double cold cores of the 35°N section in the Yellow Sea with a wave-tide-circulation coupled model. Chin. J. Oceanol. Limnol., 22(3): 292-298.
DOI:10.1007/BF02842562 |
Xu Z G, Bowen A J. 1994. Wave-and wind-driven flow in water of finite depth. J. Phys. Oceanogr., 24(9): 1850-1866.
DOI:10.1175/1520-0485(1994)024<1850:WAWDFI>2.0.CO;2 |
Yang Y Z, Qiao F L, Xia C S, Ma J, Yuan Y L. 2003. Effect of ocean wave momenfum and mixing on upper ocean. Adv.Mar. Sci., 21(4): 363-368.
(in Chinese with English abstract) |
Yang Y Z, Qiao F L, Xia C S, Ma J, Yuan Y L. 2004. Waveinduced Mixing in the Yellow Sea. Chin. J. Oceanol.Limnol., 22(3): 322-326.
DOI:10.1007/BF02842566 |
Yang Y Z, Zhan R, Teng Y. 2009. Parameterization of ocean wave-induced mixing processes for finite water depth. Acta Oceanol. Sin., 28(4): 16-22.
|
Yin X Q, Qiao F L, Yang Y Z, Xia C S, Chen X Y. 2012. Argo data assimilation in ocean general circulation model of Northwest Pacific Ocean. Ocean Dyn., 62(7): 1059-1071.
DOI:10.1007/s10236-012-0549-1 |
Yuan Y L, Pan Z D, Sun L T. 1991. LAGFD-WAM numerical wave model Ⅰ. Basic physical model. Acta Oceanol. Sin., 10(4): 483-488.
|
Yuan Y L, Qiao F L, Yin X Q, Han L, Lu M. 2012. Establishment of the ocean dynamic system with four sub-systems and the derivation of their governing equation sets. J.Hydrodyn., Ser. B, 24(2): 153-168.
DOI:10.1016/S1001-6058(11)60231-X |
Yuan Y L, Qiao F L, Yin X Q, Han L. 2013. Analytical estimation of mixing coefficient induced by surface wavegenerated turbulence based on the equilibrium solution of the second-order turbulence closure model. Sci. China Earth Sci., 56(1): 71-80.
DOI:10.1007/s11430-012-4517-x |
Yuan Y, Qiao F, Hua F, et al. 1999. The development of a coastal circulation numerical model:1. Wave-induced mixing and wave-current interaction. J. Hydrodyn. Ser. A, 14(4B): 1-8.
(in Chinese) |
Zhang T C, Yang Y Z, Yin X Q, Shi Y F, Wang Y H. 2015. Influence of wave transport flux residual on upper temperature. Adv. Mar. Sci., 33(3): 288-294.
(in Chinese with English abstract) |
Zhou W H, Yin K D, Harrison P J, Lee J H W. 2012. The influence of late summer typhoons and high river discharge on water quality in Hong Kong waters. Estuar., Coast Shelf Sci., 111: 35-47.
DOI:10.1016/j.ecss.2012.06.004 |
 2019, Vol. 37
2019, Vol. 37


