Institute of Oceanology, Chinese Academy of Sciences
Article Information
- SHI Yongfang, YANG Yongzeng, TENG Yong, SUN Meng, YUN Shengjun
- Mechanism of sea ice formation based on comprehensive observation data in Liaodong Bay, China
- Journal of Oceanology and Limnology, 37(6): 1846-1856
- http://dx.doi.org/10.1007/s00343-019-8269-8
Article History
- Received Sep. 29, 2018
- accepted in principle Nov. 26, 2018
- accepted for publication Jun. 6, 2019
2 Laboratory for Regional Oceanography and Numerical Modeling, National Laboratory for Marine Science and Technology, Qingdao 266071, China;
3 Key Laboratory of Marine Science and Numerical Modeling, Ministry of Natural Resources, Qingdao 266061, China
Historically, China, one of the countries that suffer most from the effects of sea ice, has experienced many major sea ice disasters (Yang, 2002; Sun and Shi, 2012). The impact of sea ice on channel blockages, port closures, and maritime transport disruption is becoming increasingly obvious. A sea ice disaster in 2009–2010 caused direct economic losses related to the destruction of port facilities and ships, and disrupted offshore oil and gas exploration and production, which amounted to several billion US dollars (Liu, 2017). Following the rapid development of the Bohai Rim economy, several oil production platforms have been built on the oilfields in the frozen sea area, which has come to be an important strategic base for the production of marine resources in China. Therefore, it is important to study the laws governing the growth-melt cycle of sea ice to safeguard marine resources operations, and to reduce or avoid loss of life and damage to property caused by sea ice disasters.
The formation of ice cover in a wave field has important characteristics. For example, waves not only enhance the intensity of turbulence in the upper ocean, thereby contributing to the exchange of momentum and heat between the air and the sea, but also accelerate the translational speed of sea ice for producing a larger area of open water and increasing the rate of growth of sea ice (Doble, 2007). In recent years, interest regarding wave-ice interaction has focused primarily on the dynamic interaction between waves and sea ice. For instance, sea ice is affected by waves that travel into the marginal ice zone and cause floes to raft, deform and fracture, and wave energy is attenuated through wave propagation into ice fields (Frankenstein et al., 2001; Williams et al., 2013; Zhao, 2014; Bennetts et al., 2015; Wang et al., 2016; Mosig, 2018). The effect of waves on sea ice is also important when considering thermodynamic processes. In rough sea conditions, waves agitate the frazil ice crystals such that the crystals coalesce to form nearly circular disks known as pancake ice. Given sufficient time, the pancake ice can consolidate into larger and thicker ice floes (Lange et al., 1989; Shen et al., 2001). It has been shown that wind and wave events can cause an approximate doubling of the oceanic heat fluxes in comparison with calm periods (Peterson et al., 2017).
The effects of waves on sea ice have been explored largely via experimental procedures because of a lack of simultaneous observations of waves and sea ice. For example, Shen and Ackley (1995) simulated the growth of pancake ice in a laboratory with a background two-dimensional wave field. Based on water tank tests that allowed analyses of the growth of frazil ice under the control of waves and thermal conditions, and exploration of the thermal processes associated with the transformation of grease ice to pancake ice under wave conditions, de la Rosa et al. (de la Rosa et al., 2011; de la Rosa and Maus, 2012) proposed that turbulent motion of the upper ocean is important in accelerating the rate of sea ice formation. Ogasawara et al. (2013) analyzed the thermal processes associated with the transformation of grease ice to pancake ice using a wave tank in a cold room, in which the water temperature, salinity and sea ice thickness were measured in relation to the rate of growth of sea ice.
Experimental methods can simulate the icing process over a short period only, which is generally insufficient for comprehensive investigation of the impact of waves on the rate of sea ice formation. Satellite remote sensing and observations from offshore platforms are the primary two methods used to observe sea ice in the Bohai Sea (Ji et al., 2000; Shi et al., 2002; Su and Wang, 2012; Liu et al., 2016). The parameters considered include sea ice extent, sea ice thickness and other meteorological variables; however, synchronous observations of waves and sea ice are generally lacking. Based on comprehensive observational data of the growth-melt cycle of sea ice in the coastal waters of Liaodong Bay (China) during January–March 2018, we investigated the characteristics of hydrology, meteorology and sea ice thickness during sea ice formation. Furthermore, we examined the changes in the interrelationships among heat fluxes, waves, and sea ice under actual sea conditions. The results could provide a decisionmaking support as a reference in relation to both the establishment and improvement of China's early warning system for sea ice disasters, and the protection of ice drilling operations and production platform safety.
The remainder of this paper is organized as follows. The data and methodology used in the study are described in Section 2. The characteristics of the hydrological/meteorological elements and the waveinduced turbulence during sea ice formation are presented in Section 3. The mechanism via which waves influence the thermal properties of sea ice and a summary are presented in Section 4.
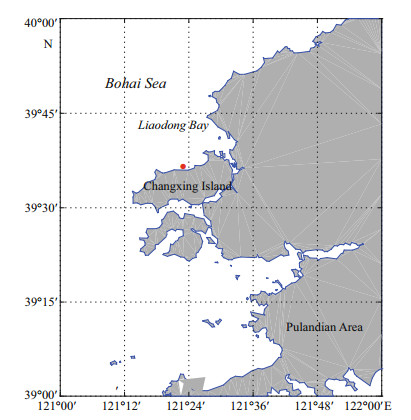
2 DATASET AND METHODOLOGY 2.1 Observation scheme and datasetThe sea ice forecast results of the satellite remote sensing monitoring and the National Marine Environmental Forecasting Center in mid-January 2018 were used, according to which the observational site was deployed at 39°36′58.31″N, 121°22′29.05″E in the north of Changxing Island, Dalian, along the coast of the Liaodong Bay, about 15 m from the ice edge line, and the water depth was 12–13 m (Fig. 1). The observation time is from January 16 to March 11, including the entire period of sea ice growth and melt. This region belongs to the temperate humid continental monsoon climate, with four distinct seasons and a large temperature difference throughout the year, dominated by one-year ice.
|
| Fig.1 The observation site (red dot) |
The observation instrument consisted of two sets of Acoustic doppler wave profile current meter of Nortek (AWAC), one was to open the simultaneous observation of the wave and sea ice, and another one to open the wave observation for the mutual verification of the first set of wave observation data. In addition, the instruments included handheld anemometer, conductivity temperature deep (CTD), and underwater photographer. The observational items included temperature, pressure, relative humidity, dew point temperature, wind speed, wind direction, ocean temperature, salinity, significant wave height, mean wave period, mean wave direction, and sea ice thickness, which we think was sufficient for the research needs.
2.2 Calculations of the heat fluxThe ice in Bohai Sea is the first-year ice, which is mainly controlled by the heat flux between the oceanatmosphere and sea ice. These thermodynamic elements include the downwelling SW radiation flux (QS), the longwave (LW) radiation flux (QL), the sensible heat flux (QH) and the latent heat flux (QE), which are calculated as follows.
2.2.1 The downwelling SW radiation fluxThe downwelling short-wave radiation flux (sum of direct and diffuse) is derived from the QS0 or "global radiation" term modified by the albedo of the surface, α, calculated for young ice (Maykut, 1982):
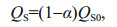
in which
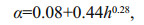
and h is the ice thickness in m. The shortwave downwelling flux is derived from basic equations:
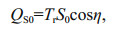
where Tr is the clear-sky transmittance, the solar constant (1 353 W/m2) and η the solar zenith angle. Though less commonly used in the literature, it is a refinement of the more-widely used model and this is adopted here:

in which ep is the water vapor pressure (in hPa or mb) at the ambient air temperature Ta.
2.2.2 The longwave (LW) radiation fluxLongwave radiation on the sea ice surface includes both absorption and reflection, and the net LW radiation is

where QLi and QLa are the LW radiation reflected and absorbed by sea ice surface, respectively. According to the law of Stefan-Boltzman,
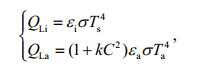
where σ is the constant of Stefan-Boltzman (5.67×108 W/(m2·K4));
TS and Ta are the temperature on sea ice surface and air temperature (K); k is the empirical coefficient with the value of 0.001 7 (George, 1986). εi and εa are the blackness of sea ice and air, and εi=0.97, 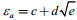
The sensible heat and latent heat between atmosphere and seawater depend mainly on the sea surface temperature, air temperature, relative humidity, wind speed, and atmospheric pressure. When sea ice has formed, the latent and sensible heat fluxes are related to the temperature difference between the atmosphere and the sea ice surface. According to the bulk formula (Lu, 1988):
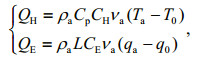
where CH and CE are the transport coefficients of sensible heat and latent heat on the surface of sea ice, respectively; CH=1.75×10-3, CE=1.75×10-3 (Hibler III, 1979; Parkinson and Washington, 1979); ρa is the air density; Cp and L are air constant-pressure specific heat and the sublimation heat of sea ice, respectively; Ta and T0 are air temperature and sea surface temperature or sea ice surface temperature; νa, qa, and q0 are the wind speed at 10 m, specific humidity and specific humidity on the sea surface or sea ice surface.
For frazil ice growth, the balanced equation of ice formation is
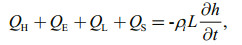
where 
The change of sea ice thickness is mainly dependent on the exchange of energy between the ocean– atmosphere and sea ice, these physical processes form the basis of the thermodynamic model of sea ice. As a kind of movement that exists at the sea-air interface at the moment, the wave has an important influence on the exchange process of momentum, heat and mass on the air-sea interface. Based on the turbulent kinetic energy model (Yuan et al., 2012), the wave-induced turbulent kinetic energy is calculated during the sea ice formation.
According to the turbulent saturation equilibrium solution based on the principle of high certainty closure (Yuan et al., 2012), the minimization of the dynamic energy dissipation rate is
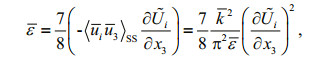 (1)
(1)where (x1,
x2,
x3) is the Cartesian coordinate system on average sea level, and the vertical axis x3 is positive upwards, k, ε are the turbulent kinetic energy and turbulent kinetic energy dissipation rate in the average sense, ui, i=1, 2, 3 is turbulent velocity, 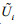
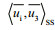
Hybrid length representation based on high deterministic closure assumptions is
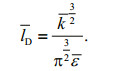 (2)
(2)Thus,
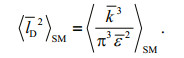 (3)
(3)From the above two formulas, we can find
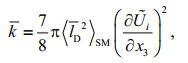 (4)
(4)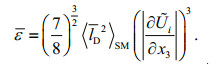 (5)
(5)The above formula 
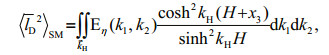 (6)
(6) (7)
(7)For the convenience of calculation, this study uses the following simplified form of the characteristic wave:
 (9)
(9)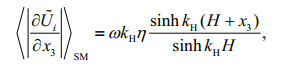 (10)
(10)where the amplitude η is 1/2 of the significant wave height, the frequency ω=2π/Tm, and the wave number kH is calculated by the finite water depth dispersion relation ω2=gkHtanh(kHH).
3 DATA ANALYSIS RESULTSThe physical process of the freezing of seawater is complex. A drop in air temperature leads to cooling of the sea surface, which means the ocean loses heat. When temperature of the surface seawater is close to the temperature of the seawater maximum density, the proportion of the upper seawater increases and thus sinks, while the proportion of the lower seawater relatively decreases and thus it rises to the surface. This process continues until the density of the water layer is even and stable. Seawater begins to freeze when its temperature drops to freezing point and heat continues to dissipate. However, wind waves can exacerbate the mixing of the upper ocean. During the process of freezing of sea ice, brine rejection occurs. This increases the salinity and density of the surrounding seawater and reduces its freezing point, which increases the difficulty of further freezing of sea ice. Brine rejection enhances the vertical mixing, which could bring up warmer water from the layer below the mixed layer. When the ocean is very shallow, as in the present case, the lower layer may not exist and the process of brine rejection is not discussed in this paper. Based on comprehensive observational data, in the following sections, we analyze the characteristics of the meteorological and hydrological elements during the freezing of sea ice and examine the vertical variation of ocean temperature under wave conditions.
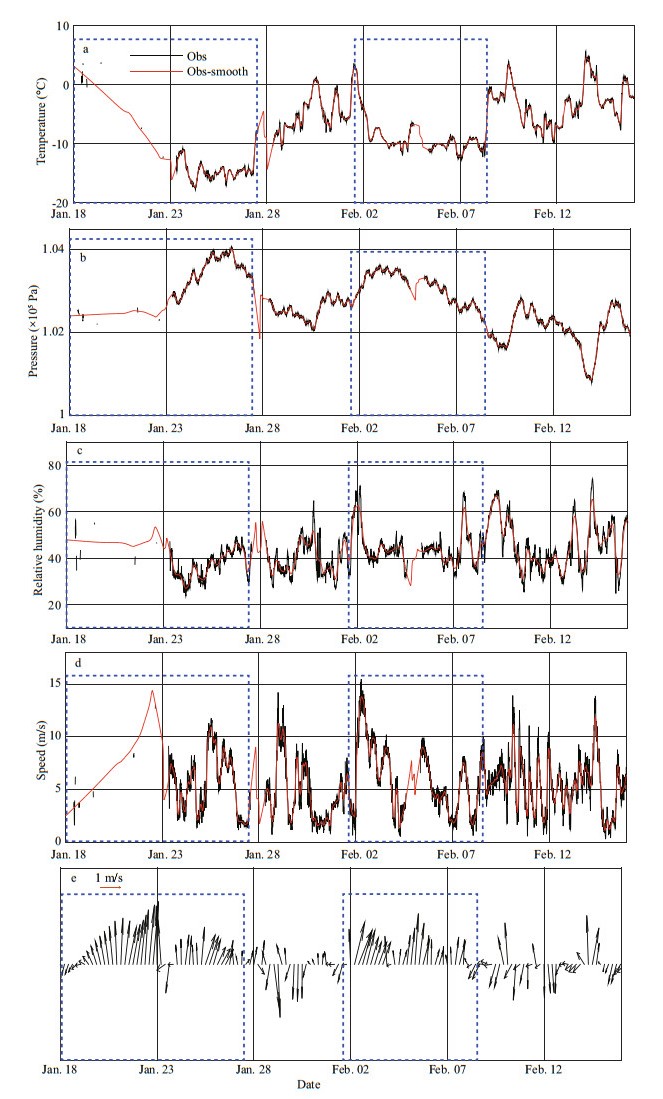
3.1 Sea ice thickness and meteorological factorsDuring the freezing of seawater in the study period, the air temperature exhibited a two-stage cooling cycle (Fig. 2a). The first drop in air temperature occurred slowly from 12:00 local time (LT) on January 18 to 23:50 LT on January 22, 2018, and the duration of the low-temperature period was about 96 h. The second stage of air temperature cooling occurred rapidly from 12:00 LT on February 1 to 08:00 LT on February 2, 2018, and the air temperature remained low until it began to rise after approximately 144 h. Corresponding to the two falls in air temperature, atmospheric pressure exhibited an upward trend, reaching a maximum value of 1.04×105 Pa (Fig. 2b), whereas the relative humidity showed no significant trend of change (Fig. 2c). The wind speed was strong during the process of the drop in ocean temperature (max: 15 m/s). Strong wind speed not only increases the surface roughness of the ocean, which pushes the atmosphere-ocean exchange of heat flux, but it also mixes the seawater, facilitating rapid ocean cooling. Meanwhile, the wind direction may be also important for the sea ice formation: i.e., onshore winds push sea ice toward the coast and increase thickness, and vice versa. The observation point is located near the shore to the South and open water to the north. During the two cooling processes, the south wind is dominant, which will make the sea ice drift away from the shore. Because of the shallow water depth at the observation point and the fast freezing near the shore, the observations show that sea ice is relatively flat and almost no overlap. It should be noted that few meteorological data were acquired during January 18–23; however, the fluctuation of the time series of the variables was reduced by smoothing the data (Fig. 2).
|
| Fig.2 Changes of meteorological factors during sea icing |
It can be seen from Fig. 3 that the sea ice began to form about five days after the initial drop in air temperature on January 18. However, the air temperature did not remain depressed and the sea ice thickness did not increase until the second drop in air temperature on February 1, following which the thickness of the sea ice increased rapidly to reach a maximum value of 60 cm. In summary, air temperature has a critical role in the formation of sea ice, but sea ice formation lags a change in air temperature. It takes a long time from when seawater reaches freezing point for sea ice to start to form, whereas the time required for sea ice to reach a certain thickness after initial formation is comparatively short.

|
| Fig.3 Changes of sea ice thickness |
Heat exchange at the atmosphere-ocean interface has a vital role in the growth-melt cycle of sea ice. Therefore, it is necessary to calculate and analyze the relevant thermodynamic elements. Our observation points refer mostly to flat ice, and the effect of movement of floating ice on the rate of sea ice growth is ignored here. In this study, we calculated the heat fluxes such as shortwave (SW) radiation flux, longwave (LW) radiation flux, latent heat, and sensible heat, and the changing relationships between the thermodynamic elements and sea ice thickness are discussed in this paper.
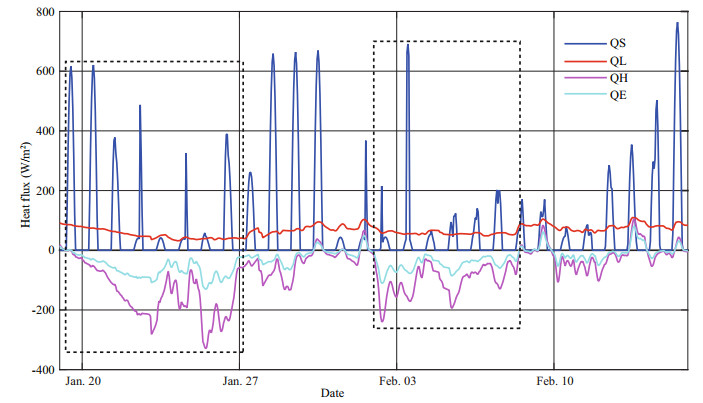
As shown in Fig. 4, the amplitude of the change in SW radiation flux on the ice surface was large because of the amount of total cloud cover and the absorption of SW radiation after the formation of sea ice. Conversely, the change in LW radiation flux was reasonably small. However, both SW and LW radiation constitute the main source of the positive heat flux at the ice surface. Affected by the atmosphereocean temperature difference, latent heat and sensible heat at the sea ice surface showed considerable variation. During the two cooling episodes, the amplitude of latent heat and sensible heat was large, which caused the ocean to lose heat rapidly. With reference to the change in observed ice thickness (Fig. 3), it can be seen that the ocean lost most heat in the first episode of cooling (January 18–27), mainly through open water, which could have been crucial to the formation of sea ice on January 28. The intensity of cooling in the second episode was weaker than in the first, and both the sensible heat and the latent heat were relatively small in comparison with the first episode. However, prior to that, the seawater temperature was already near freezing, and the thickness of the sea ice increased rapidly during this stage and it maintained a large value. The atmosphereocean-ice heat exchange dominates the growth-melt cycle of sea ice. However, the change in sea ice lags the changes in thermodynamic elements because the variation in sea ice thickness is related not only to the heat flux at the atmosphere-ocean-ice interface but also to the dynamic processes of the upper ocean.
|
| Fig.4 Time series of heat flux between the ocean-atmosphere and sea ice |
There are two conditions necessary for sea ice to form: the ocean temperature must reach freezing point and the upper ocean must be evenly mixed. Therefore, in addition to meteorological factors, sea surface waves have an essential influence on the rate of sea ice formation. In many cases, sea ice can grow under turbulent ocean conditions (Weeks and Ackley, 1982). This process can be divided into three stages: (1) formation of tiny frazil crystals kept in suspension in the upper ocean by wind- and wave-generated turbulence; (2) accumulation of a surface frazil-ice or grease-ice layer when the turbulence ceases; and (3) freeze-up of the mush into a cover of solid ice. Under the presence of a wave field, stage (3) is often accompanied by the formation of ice pancake that grow in size and thickness before eventually coalescing. During the studied period, the first drop in air temperature of about 20℃ persisted for about 108 h, i.e., from 12:00 LT on January 18 to 23:50 LT January 22. At this time, the ocean temperature continued to decrease. Frazil ice appeared on the sea surface on January 22. The frazil ice then accumulated into the form of pancake ice, which was frozen into the form of ice caps on January 25 (Fig. 5).

|
| Fig.5 Formation of sea ice (photos were taken by digital camera during the observation) |
As shown in Fig. 6, the significant wave height had a large value (max.: 1.8 m) before the sea began to freeze, but it gradually decreased as the surface frazilice or grease-ice layer accumulated into ice caps. The processes of wave-induced turbulence and wave transport flux residual have considerable impact on the upper ocean. The dynamic process of waves causes the ocean surface to be exposed continuously to the cold air, which maintains a high atmosphereocean heat flux that might result in the development of more ice than under calm sea conditions. To analyze the influence of waves on the upper ocean during the process of sea icing, we calculated the wave-induced turbulent kinetic energy based on the turbulent saturation equilibrium solution of Eqs.1–10, given the high deterministic closure principle in the wave kinetic energy model (Yuan et al., 2012). For quality control of the sea temperature profile data, values that were greater than ±3 standard deviations from the average of the five nearest points were eliminated, and then the remaining profile data were smoothed using a five-point moving average.

|
| Fig.6 Changes of the significant wave height |
It is suggested that the upper ocean temperature dropped rapidly to form an inverse thermocline (09:00 LT on January 19) at the beginning of the first drop in air temperature (Fig. 7). The ocean was mixed convectively because of the low temperature of the surface seawater and the comparatively high temperature of the seawater in the lower layer. At this time, the wind and waves were severe, which would have enhanced upper-ocean mixing. The lower ocean temperature continued to decrease from -0.55℃ on January 19 to -1.75℃ on January 25, and the temperature difference between the upper and lower ocean became smaller, with magnitude of about 10-2. When a stable ice cover had formed on the sea surface, the profile of ocean temperature was smooth and the seawater under the sea ice was stable. The trend of wave-induce turbulent kinetic energy first increased and then decreased. At the beginning of the drop in air temperature, the maximum value of wave-induced turbulent kinetic energy was 5×10-3 k/(m2·s2); however, it was close to zero at the depth of 2 m, which was about the depth of influence of the waves. Then, it reached a maximum value of 0.5 k/(m2·s2) with a depth of influence of about 4 m during the period of frazil ice on January 21–22. The wave-induced turbulent kinetic energy then reduced quickly to 2.5×10-3 k/(m2·s2) up until January 23 when the ice cover had formed. The above analysis identifies that wave-induced turbulent kinetic energy was considerable before the sea ice froze, which could have strengthened the intensity of turbulence in the upper ocean. This would have enhanced the atmosphere-ocean exchange of momentum and heat, which would have accelerated the rate of sea ice formation.

|
| Fig.7 Vertical variations of wave-induced turbulent kinetic energy and ocean temperature |
It has been found that upper-ocean turbulence can be induced by the physical process of wave shear, which results in deepening of the upper mixed layer and allows the mixed layer to stabilize at an accelerated rate (Babanin and Haus, 2009; Yang et al., 2009; Dai et al., 2010; Huang et al., 2011; Yuan et al., 2013). Based on in situ measurements in the Weddell Sea, Doble (2007) found that in comparison with calm conditions, sea ice could grow twice as quickly under conditions with waves. Wang et al. (2008) reached the same conclusion based on tank experiments. However, studies of the growth-melt cycle of sea ice under conditions with waves are generally based on laboratory experiments because of the lack of observational data. This study used comprehensive observational data acquired in the coastal waters of Liaodong Bay (China) to examine the effects of hydrological and meteorological characteristics and wave-induced turbulent kinetic on the process of seawater freezing.
Analysis suggested that the heat flux between the atmosphere-ocean and sea ice plays a vital role during the freezing process, and that it leads the change of sea ice thickness. Although it takes a long time from when seawater reaches freezing point for sea ice to start to form, the time for sea ice to reach a certain thickness after initial formation is comparatively shorter. Sea ice formation depends on two primary conditions: an ocean temperature at freezing point and an evenly mixed upper ocean. In addition to meteorological factors, sea surface waves also have an important influence on the rate of sea ice formation. Wave-induced turbulent kinetic energy can be considerable before sea ice starts to freeze, which can strengthen the intensity of upper-ocean mixing and cause the sea surface to be exposed continuously to cold air. Consequently, in comparison with calm sea conditions, greater sea ice development could occur when high atmosphere-ocean heat flux is maintained under sea conditions with waves.
The contribution of waves is generally not considered in sea ice models because that the effect of waves on sea ice can be neglected away from the ice edge zone. However, the physical process of waves must be considered in the ice margin zone. In future work, we will consider the influence of waves on the formation of sea ice using numerical models. In combination with the theoretical mechanism of surface waves, a parameterized scheme for coupling wave-sea ice thermodynamics will be established. Based on a thermodynamic-dynamic sea ice model that considers wave processes, the capacity of the model to simulate sea ice processes of rapid freezing and ablation will be tested. The results of this project could ultimately provide decision-making support and act as a reference in relation to both the establishment and improvement of China's early warning system for sea ice disasters, and the protection of ice drilling operations and production platform safety.
5 DATA AVAILABILITY STATEMENTThe datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Babanin A V, Haus B K. 2009. On the existence of water turbulence induced by nonbreaking surface waves. Journal of Physical Oceanography, 39(10): 2 675-2 679.
DOI:10.1175/2009JPO4202.1 |
Bennetts L G, O'Farrell S, Uotila P, Squire V A. 2015. An idealized wave-ice interaction model without subgrid spatial or temporal discretizations. Annals of Glaciology, 56(69): 258-262.
DOI:10.3189/2015AoG69A599 |
Dai D J, Qiao F L, Sulisz W, Han L, Babanin A. 2010. An experiment on the nonbreaking surface-wave-induced vertical mixing. Journal of Physical Oceanography, 40(9): 2 180-2 188.
DOI:10.1175/2010JPO4378.1 |
de la Rosa S, Maus S, Kern S. 2011. Thermodynamic investigation of an evolving grease to pancake ice field. Annals of Glaciology, 52(57): 206-214.
DOI:10.3189/172756411795931787 |
de la Rosa S, Maus S. 2012. Laboratory study of frazil ice accumulation under wave conditions. The Cryosphere, 6(1): 173-191.
DOI:10.5194/tc-6-173-2012 |
Doble M J. 2007. Growth and Motion at the Weddell Sea Ice Edge. University of Southampton, UK.
|
Frankenstein S, Loset S, Shen H H. 2001. Wave-ice interactions in Barents Sea marginal ice zone. Journal of Cold Regions Engineering, 15(2): 91-102.
DOI:10.1061/(ASCE)0887-381X(2001)15:2(91) |
George D A. 1986. River and Lake Ice Engineering. Book Craflers Inc., Chelseas Michigan. p.216-227.
|
Hibler III W D. 1979. A dynamic thermodynamic sea ice model. Journal of Physical Oceanography, 9(4): 815-846.
DOI:10.1175/1520-0485(1979)009<0815:ADTSIM>2.0.CO;2 |
Huang C J, Qiao F L, Song Z Y, Ezer T. 2011. Improving simulations of the upper ocean by inclusion of surface waves in the Mellor-Yamada turbulence scheme. Journal of Geophysical Research:Oceans, 116(C1): C01007.
DOI:10.1029/2010JC006320 |
Ji S Y, Yue Q J, Zhang X. 2000. Thermodynamic analysis during sea ice growth in the Liaodong Bay. Marine Environmental Science, 19(3): 35-39.
(in Chinese with English abstract) |
Ji S Y, Yue Q J. 2000. Discussion on sea ice diagnostic thickness for the Bohai Sea. Acta Oceanologica Sinica, 22(6): 117-123.
(in Chinese with English abstract) |
Lange M A, Ackley S F, Wadhams P, Dieckmann G S, Eicken H. 1989. Development of sea ice in the Weddell Sea. Annals of Glaciology, 12: 92-96.
DOI:10.3189/S0260305500007023 |
Liu W S, Sheng H, Zhang X. 2016. Sea ice thickness estimation in the Bohai Sea using geostationary ocean color imager data. Acta Oceanologica Sinica, 35(7): 105-112.
DOI:10.1007/s13131-016-0910-1 |
Lu Q M. 1988. On Mesoscale Modelling of the Dynamics and Thermodynamics of Sea Ice. Technical University of Denmark, Copenhagen. p.50-73.
|
Maykut G A. 1982. Large-scale heat exchange and ice production in the central Arctic. Journal of Geophysical Research:Oceans, 87(C10): 7 971-7 984.
DOI:10.1029/JC087iC10p07971 |
Mosig J E M. 2018. Contemporary wave-ice interaction models. University of Otago, Danidine.
|
Ogasawara T, Ogasawara A, Sakai S. 2013. Thermodynamics on grease-pancake ice growth in a sea ice-wave tank. In: Proceedings of the Twenty-third (2013) International Offshore and Polar Engineering. International Society of Offshore and Polar Engineers, Anchorage, Alaska.
|
Parkinson C L, Washington W M. 1979. A large-scale numerical model of sea ice. Journal of Geophysical Research:Oceans, 84(C1): 311-337.
DOI:10.1029/JC084iC01p00311 |
Peterson A K, Fer I, McPhee M G, Randelhoff A. 2017. Turbulent heat and momentum fluxes in the upper ocean under Arctic sea ice. Journal of Geophysical Research:Oceans, 122(2): 1 439-1 456.
DOI:10.1002/2016JC012283 |
Shen H H, Ackley S F, Hopkins M A. 2001. A conceptual model for pancake-ice formation in a wave field. Annals of Glaciology, 33: 361-367.
DOI:10.3189/172756401781818239 |
Shen H H, Ackley S F. 1995. A laboratory-produced pancake ice cover in a two-dimensional wave field. Antarctic Journal, 30: 106-107.
|
Shi P J, Fan Y D, Ha S, Yuan Y, Xie F. 2002. Calculating gross sea ice resource using AVHRR and MODIS data. Journal of Natural Resources, 17(2): 138-143.
(in Chinese with English abstract) |
Su H, Wang Y P. 2012. Using MODIS data to estimate sea ice thickness in the Bohai Sea (China) in the 2009-2010 winter. Journal of Geophysical Research:Oceans, 117(C10): C10018.
|
Sun S, Shi P J. 2012. Risk assessment of sea ice disaster in Bohai Sea and north Yellow Sea of China. Journal of Natural Disasters, 21(4): 8-13.
(in Chinese with English abstract) |
Wang R, Shen H H, Evers K U. 2008. An experimental study of wave induced ice production. In: Proceedings of the 19th IAHR International Symposium on Ice. Vancouver, Canada.
|
Wang Y, Holt B, Rogers W E, Thomson J, Shen H H. 2016. Wind and wave influences on sea ice floe size and leads in the Beaufort and Chukchi Seas during the summer-fall transition 2014. Journal of Geophysical Research:Oceans, 121(2): 1 502-1 525.
DOI:10.1002/2015JC011349 |
Weeks W F, Ackley S F. 1982. The Growth, Structure, and Properties of Sea Ice. U.S. Army Cold Regions Research and Engineering Laboratory, Hanover, NH, 82-100.
|
Williams T D, Bennetts L G, Squire V A, Dumont D, Bertino L. 2013a. Wave-ice interactions in the marginal ice zone.Part 1:theoretical foundations. Ocean Modelling, 71: 81-91.
DOI:10.1016/j.ocemod.2013.05.010 |
Williams T D, Bennetts L G, Squire V A, Dumont D, Bertino L. 2013b. Wave-ice interactions in the marginal ice zone.Part 2:numerical implementation and sensitivity studies along 1D transects of the ocean surface. Ocean Modelling, 71: 92-101.
DOI:10.1016/j.ocemod.2013.05.011 |
Yang H T. 2002. Marine disasters and its reduction in the last 10 years. Marine Forecasts, 19(1): 2-8.
(in Chinese with English abstract) |
Yang Y Z, Zhan R, Teng Y. 2009. Parameterization of ocean wave-induced mixing processes for finite water depth. Acta Oceanologica Sinica, 28(4): 16-22.
|
Yuan Y L, Qiao F L, Yin X Q, Han L, Lu M. 2012. Establishment of the ocean dynamic system with four sub-systems and the derivation of their governing equation sets. Journal of Hydrodynamics, 24(2): 153-168.
DOI:10.1016/S1001-6058(11)60231-X |
Yuan Y L, Qiao F L, Yin X Q, Han L. 2013. Analytical estimation of mixing coefficient induced by surface wavegenerated turbulence based on the equilibrium solution of the second-order turbulence closure model. Science China Earth Sciences, 56(1): 71-80.
|
Zhao X. 2014. Wave Propagation under Ice Covers. Ph.D Dissertation. Clarkson University, ProQuest Dissertation Publishing.
|
 2019, Vol. 37
2019, Vol. 37


