Institute of Oceanology, Chinese Academy of Sciences
Article Information
- YUE Che, LI Jingkai, GUAN Changlong, LIAN Xihu, WU Kejian
- Surface wave simulation during winter with sea ice in the Bohai Sea
- Journal of Oceanology and Limnology, 37(6): 1857-1867
- http://dx.doi.org/10.1007/s00343-019-8253-3
Article History
- Received Sep. 19, 2018
- accepted in principle Jan. 3, 2019
- accepted for publication Jan. 25, 2019
2 North China Sea Marine Forecasting Center, Ministry of Natural Resources (MNR), Qingdao 266000, China
Sea ice in the Arctic Ocean has experienced a rapid reduction over the last 40 years as a result of climate change (Stroeve et al., 2012; Serreze and Stroeve, 2015) with subsequent consequences of more dynamic sea ice conditions and increasing wave-ice interactions (Thomson and Rogers, 2014; Thomson et al., 2018). Thus, theoretical, observational and numerical developments regarding wave propagation through ice-covered waters have accelerated in the last 20 years. Propagating through ice covers, waves will be scattered and dissipated, which are very different from the usual open water cases (Squire, 2007). Hence, accounting for the ice effects on waves has become a precondition to simulate waves in icecovered sea areas accurately. However, almost all simulations to-date have focused on waves in polar regions (Doble and Bidlot, 2013; Khon et al., 2014; Li et al., 2015; Rogers et al., 2016; Cheng et al., 2017) where wave-ice interactions play a potential role in the study of climate. In contrast, wave-ice theories are rarely applied in the wave simulations of nearshore sea areas in the middle latitudes, which limits knowledge on waves when sea ice does occur in these regions. In fact, information on nearshore wave conditions are necessary to guide human industrial and economic activities during winter.
The Bohai Sea is the northernmost marginal sea of China where some sea water freezes annually from December to March. Wave conditions in the Bohai Sea are highly related to shipping, fishing, oil extraction and other human activities; thus, several wave studies using numerical wave models have been performed (Huang, 2009; Shi et al., 2011; Lv et al., 2014; Wang et al., 2016) and can provide an ampler source of wave information than direct measurements. These studies were usually carried out by Simulating Waves Nearshore (SWAN) model (Booij et al., 1999) that properly accounts for shallow water wave processes and employs a finite difference approach based on the so-called method of lines for discretization of the action balance equation (The SWAN team, 2018). Thus it may be more suitable for nearshore waters than other popular 3rd generation wave models, such as WaveWatch Ⅲ (Tolman, 1991) (WW3) and Wave Action Model (The WAMDI Group, 1988) (Lv et al., 2014; Amrutha et al., 2016). Moreover, parameterizations of various source terms are also improved when applying the SWAN model in the Bohai Sea (Yin et al., 2005; Wang et al., 2012). However, during the freezing interval in winter, knowledge of waves remains insufficient because the SWAN model itself has no representation of sea ice even in the latest version 41.20.
To improve such a situation, in this study, we implemented an eddy viscosity wave-ice theory into the SWAN model (named SWAN-ice) and then analyzed the sea ice effect on Bohai Sea surface waves based on hindcasted results. The organization of the paper is as follows. Section 2 describes the model setups, including the forcing data information and the wave-ice parameterization. Section 3 shows the comparison of wave height between the measured by buoy and the simulated by the SWAN-ice. Section 4 provides the hindcasted results and the discussions of waves in ice-covered waters in the Bohai Sea. Conclusions and recommendations for further studies are given in Section 5.
2 METHODThe SWAN v41.20 model, developed by the Delft University of Technology to compute random, shortcrested wind-generated waves in coastal regions and inland waters (http://www.swan.tudelft.nl/), was applied to compute the evolution of wave action density. The wave action density, N (x, y, t; σ, θ) is a function of space (x and y), time (t), frequencies (σ) and propagation direction (θ). Its evolution is governed by
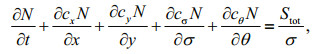 (1)
(1)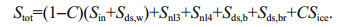 (2)
(2)In this study, there were seven processes that, in total, contributed to Stot in Eq.2: wave growth by wind Sin (Komen et al., 1994), nonlinear transfer of wave energy through three-wave interactions Snl3 (Eldeberky and Battjes, 1996) and four-wave interactions Snl4 (Hasselmann et al., 1985), wave decay due to whitecapping Sds, w (Komen et al., 1984), bottom friction Sds, b (Hasselmann et al., 1973), depth-induced wave breaking Sds, br (Battjes and Janssen, 1978) and ice effect on waves Sice which was additionally added in this study and will be clarified in Section 2.2. Compared with the original SWAN, sea ice concentration (C) was adopted to scale the source terms. As Eq.2 shows, Sin and Sds, w were both scaled by the fraction of open water (1–C) and Sice was scaled by C. The other terms are the same as for open water cases (Cheng et al., 2017).
The computational domain was defined (28°– 42°N, 117°–132°E) by applying a regularly spaced latitude-longitude grid with 0.05° grid spacing. The spectra are composed of 24 directions and 32 frequencies discretized from 0.05 to 0.96 Hz on a logarithmic scale.
2.1 Forcing dataWe used the ETOPO1 bathymetry data (https://www.ngdc.noaa.gov/mgg/global/global.html) and interpolate them to the 0.05°×0.05° mesh grid. Sea surface wind and ice thickness data were from the National Centers for Environmental Prediction's Climate Forecast System version 2 (CFSv2) selected hourly time-series products (https://rda.ucar.edu/datasets/ds094.1/#). The spatial resolutions for surface wind and ice thicknesss were approximately 0.2° and the time resolutions were 1 h and 24 h, respectively. Daily average ice concentration was obtained from the National Snow and Ice Data Center's MASIE-AMSR2 (MASAM2) 4-km product (http://nsidc.org/data/G10005).
2.2 Wave-ice termIn general, ice of different types and sizes will affect waves in different ways and change the dispersion relation in open water. These ice effects on waves (e.g. wave scattering, attenuation) have been implemented in the WW3 model as an independent source term (The WAVEWATCH-Ⅲ Development Group, 2016). Using this as a basis, we added a waveice term Sice in the action balance equation of the SWAN model to improve its capability of simulating waves in ice-covered waters. According to observations in the Arctic marginal ice zone (Cheng et al., 2017), the ice effect on wave speed is not significant, hence for simplicity, only wave damping by ice was considered. Here, we adopted an eddy viscosity wave-ice model (EVWI) (Liu and MolloChristensen, 1988; Liu et al., 1991, 1992) which is also named IC2 in the WW3 to describe such wave damping. In the EVWI, ice is regarded as a continuous thin elastic plate and dissipation is caused by friction in the boundary layer below the ice. Among several wave-ice models, EVWI was chosen because (1) it shows frequency dependent wave damping consistent with field measurements (Meylan et al., 2014; Doble et al., 2015; Rogers et al., 2016), (2) the physical assumptions are more suitable for sea ice cover in the Bohai Sea than scattering theories consuming conservative wave energy (Zhao et al., 2015), (3) compared with the viscoelastic wave-ice model (Wang and Shen, 2010), EVWI is more easily to be implemented into the SWAN model with more computational efficiency and (4) it showed a good performance in previous wave hindcasts (Liu et al., 1991; Li et al., 2015).
Taking the parameterization of EVWI in WW3 as a reference, the Sice term, including the damping of sea ice on the wave spectrum energy and the modified dispersion relation, is expressed as
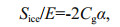 (3)
(3)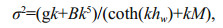 (4)
(4)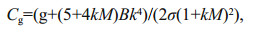 (5)
(5)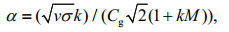 (6)
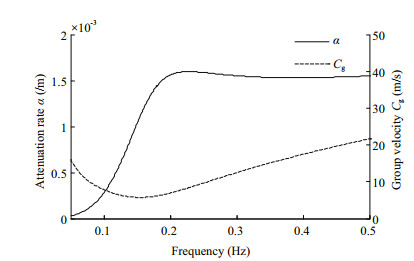
(6)where the variables B=(EIh3/(12(1–s2)ρw)) and M=hρI/ρw quantify the effects of ice bending and inertia, respectively, E is energy density spectrum (E/σ=N), α is the exponential decay rate (Wadhams et al., 1988), k is wave number, h is the ice thickness, Cg is group velocity and hw is the water depth. Other constant parameter settings are: s=0.3 (Poisson's ratio), EI=6×109 N/m2 (Young's modulus of sea ice), g=9.81 m/s2 (gravitational acceleration), ρw= 1 025 kg/m2 (water density), ρI=0.9ρw (ice density) and ν=10-2 m2/s (eddy viscosity) (Liu et al., 1991). With the above parameterization of Sice, we first solved the new dispersion relation in Eq.4 by bisection iteration and then substituted the solved k into Eqs.5 and 6 to get the exponential decay rate α which is used to describe the ice-induced wave attenuation. An example of how the calculated α and Cg change as a function of wave frequencies are presented in Fig. 1. It shows a rapid increase in α with increasing frequency until frequency is > 0.2 Hz, which is consistent with the simulation in Liu et al. (1991).
|
| Fig.1 Attenuation rate (α) and group velocity (Cg) versus wave frequency for EVWI Ice thickness (h=0.2 m) and water depth (hw=100 m) were assumed to be constant. |
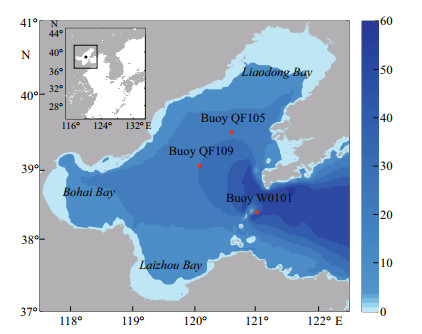
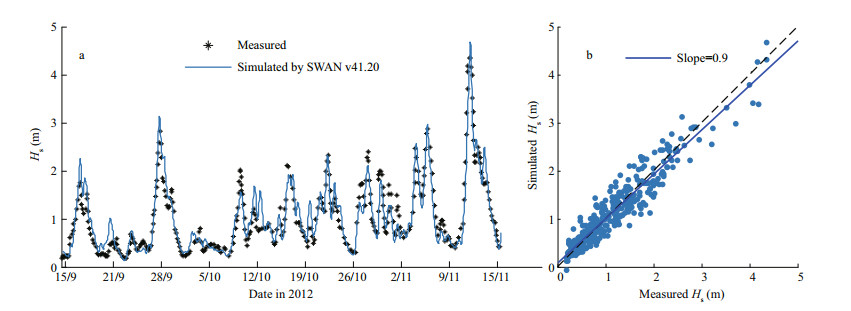
To ensure the accuracy of the wave simulations, we first validated the simulation for open water cases by comparing the simulated significant wave height Hs with records from the W0101 buoy, located at the Bohai Strait and shown as a red cross in Fig. 2. As the default model settings of SWAN usually are not optimal for the Bohai Sea (Yin et al., 2005; Lv et al., 2014), we adopted 1.1×10-5 as the coefficient of rate of whitecapping dissipation Cds in Sds, w term which is similar as Huang (2009) did to minimize the root mean square error (RMSE). The comparison results showed that the simulated Hs agreed well with measurements exhibiting a correlation coefficient 0.95 (Fig. 3). With the good performance of hindcasting waves in ice-free water, we then checked the capability of SWAN-ice for modeling waves in ice-covered areas in the Bohai Sea.
|
| Fig.2 Bathymetry of the Bohai Sea and the computational domain The shaded blues bars represent water depth (m) and the red crosses represent the oceanographic buoy sites. |
|
| Fig.3 Time series comparison (a) and scatter plot (b) between measured (buoy W0101) and simulated Hs from the Bohai Sea spanning 15 September to 15 November 2012 a. the black stars represent direct measurements, and the blue curve represents the simulation; b. the black dashed line is a 1:1 line, and the blue solid line represents the least square fit. |
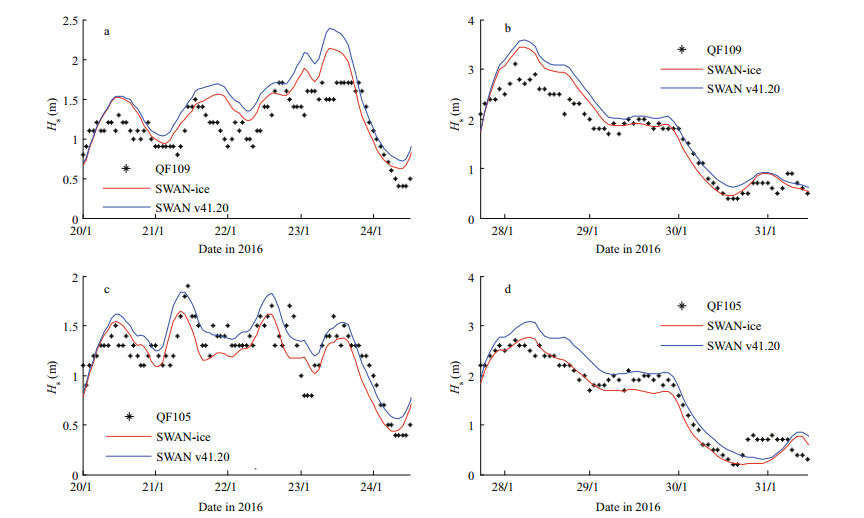
Usually, sea ice in the Bohai Sea appears in the middle of November and disappears by the end of March (~130 days duration) and is mainly concentrated in the Liaodong Bay where continuous ice sheets and pancake ice are dominant (Zhang et al., 2007). With large ice coverage, for example it is more than 1.4×104 km2 on average during January and February in 2016, the wave evolution in the Bohai Sea must be significantly influenced by the sea ice. This influence can be described by the SWAN-ice model, but we were unable to perform a validation, because unfortunately there was no available buoy and altimeter-derived wave data under the ice cover in the Bohai Sea. Hence, we could only evaluate the SWANice with data from buoys (QF105 and QF109, shown as red crosses in Fig. 2) near the ice edge where the ice effect on waves still can be distinguished to some extent, especially with an offshore wind. This is because the effective fetch between the coastline and two buoys is shortened due coastal sea ice (Gemmrich et al., 2018). Thus the real Hs should be smaller than simulated by the ice-free SWAN model. To verify this idea, we compared the measured and simulated Hs at two locations (buoy QF105 and QF109) from 16 January to 28 February 2016 with SWAN 41.20 and the SWAN-ice, respectively. Figure 4 displays time series comparisons during two offshore wind periods and Fig. 5 displays the scatter plots for all offshore wind cases. As expected, the results of the SWAN-ice model with smaller values better fit the measured Hs than SWAN v41.20 and the least square fitting line was closer to the idea value 1. When we calculated the relative error of simulated Hs for the whole time interval, we found that the SWAN-ice model reduced it from 10.42% to 1.71%. Other error information, including bias and RMSE are shown in Table 1; these all indicated that the accuracy of simulated Hs near the ice edge in the Bohai Sea was improved. Therefore, we speculate that the accuracy of simulated waves in the ice-covered waters of the Bohai Sea was improved as well. However, for 23–24 and 28–29 January at the QF109 location, even with the SWAN-ice the simulation was still much larger than the direct measurements as Fig. 4a & b shows, it may results from the low resolution of the forcing wind which is not able to capture the small-scale variability. And physically, the SWAN-ice indeed makes more sense by considering wave damping caused by sea ice. Hereafter, we proceed discussing the waves during winter in the Bohai Sea with the SWAN-ice model. For SWAN 41.20, we should notice that the accuracy of simulated Hs at buoy locations can also be improved to some extent by regarding the ice cover as land to shorten the fetch. Nevertheless, this approach introduces many uncertainties of artificial factor and ignores sea ice variations in time and space, so it is not discussed here.
|
| Fig.4 Time series comparisons between measured (QF105 and QF109) and simulated (SWAN v41.20 and SWAN-ice) Hs from the Bohai Sea The black stars are buoy measurements for QF109 (a, b) and QF105 (c, d), and the blue and red curves are simulations with SWAN v41.20 and SWAN-ice, respectively. |

|
| Fig.5 Scatter plot showing measured (QF105 and QF109) and simulated (SWAN-ice) Hs from the Bohai Sea The black dashed line is a 1:1 line. The solid blue and red lines represent the least square fits for the results of SWAN v41.20 (not shown) and the SWAN-ice, respectively. |

|
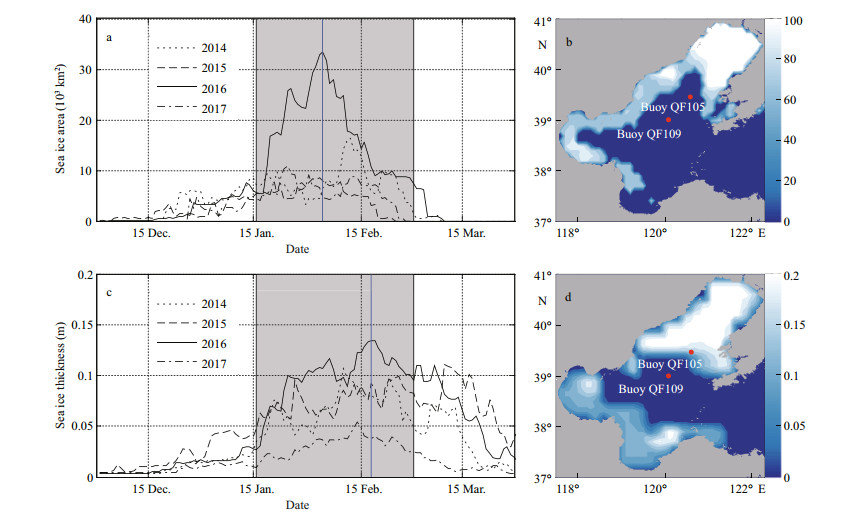
According to previous studies (Tang et al., 2012), sea ice in the Bohai Sea shows a clear annual variation. Its intensity decreased from the 1950s to 1990s, while it has intensified since 2000. From MASAM2 and CFSv2 data, Fig. 6a & c show the ice coverage (sea area × ice concentration) and mean ice thickness from 2014 to 2017, respectively. And it is easy to find that the ice conditions in 2016 were the severest among recent years with largest sea ice area and ice thickness. Two corresponding examples of spatial distributions of ice coverage and ice thickness are shown as contours in Fig. 6b & d. Due to the lower resolution of the CFSv2 data, variations in ice thickness do not correspond well with ice concentration (Fig. 6). However, this will not influence the judgement of whether a grid is covered by ice because only ice concentration is used to scale source terms in the governing equation (Eq.2), and ice thickness data are interpolated to the grid only when ice concentrations are greater than zero. Therefore, according to MASAM2 ice data shown in Fig. 6a, in the following wave study, we will first focus on the winter from 16 January to 28 February 2016 that exhibited large ice extent, expecting that the ice influence on waves would be significant.
|
| Fig.6 Sea ice coverage (a) and mean thickness (c) in the Bohai Sea spanning 2014 to 2017; (b) and (d) are the spatial distributions of the maximum ice coverage (%) and thickness (m) in 2016 respectively Shaded areas in (a) and (c) correspond to the time covered by the wave simulations. |
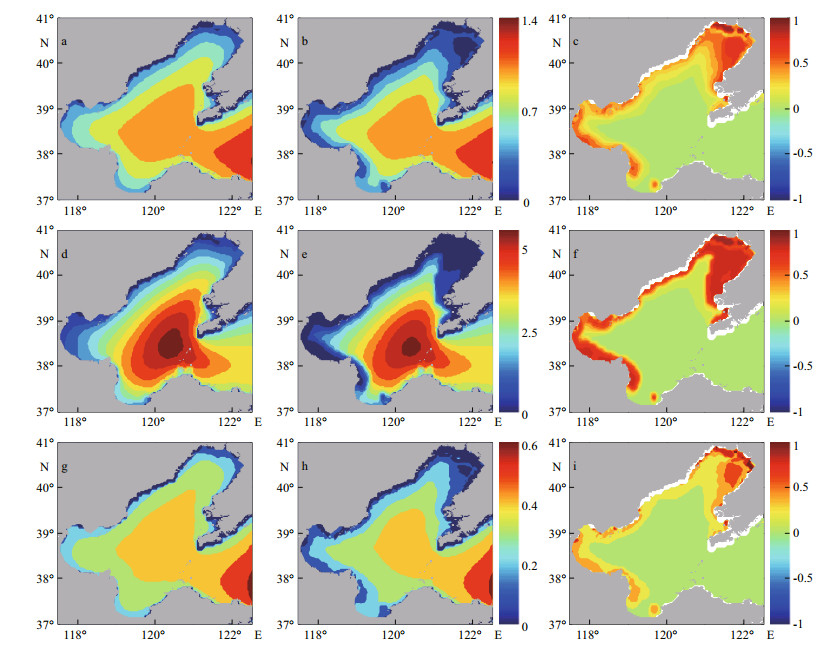
Applying SWAN v41.20 and SWAN-ice models, the simulated averaged Hs from 16 January to 28 February 2016 are shown in Fig. 7a & b respectively, and Fig. 7c shows the relative difference (RvdH, expression in Table 2). As expected, although both of the models demonstrate similar Hs distributions, Hs in Liaodong Bay and west of Laizhou Bay are much smaller (Fig. 7b) due to the existence of sea ice. To further understand such decrease of Hs, we also showed averaged Hs during stormy and calm cases separately in Fig. 7d, e, g & h, because there may be different wave evolution behaviors in partially icecovered waters in these two situations (Li et al., 2015). Here, the stormy and calm cases were defined by the averaged Hs of the Bohai Sea larger than 3 m and smaller than 0.5 m, respectively. Then by calculating the absolute difference of Hs (AvdH) and RvdH, we found that the ice effect on simulated Hs was more prominent for stormy conditions. As shown in Fig. 7f & i, the RvdH for storms was obviously larger than that for calm cases. As a frequency dependent wave-ice model, EVWI itself shows no advantage on damping stronger waves, so we think this phenomenon may be related to other physical processes. For example, in ice-covered water, if there is no representation of ice in the model, winds will input more energy to surface waves leading to a high growth rate of Hs during storms. But such input energy is blocked by the ice cover in the SWAN-ice, thus resulting in larger calculated RvdH shown in Fig. 7f. However, we still remain caution with this interpretation since wave-ice interactions are complicated, and a more comprehensive source term analysis is needed to check the detailed reasons in further study.
|
| Fig.7 Average Hs (m) simulated by SWAN v41.20 (a, d, g) and the SWAN-ice (b, e, h) in the Bohai Sea from 16 January to 28 February 2016 with relative differences RvdH (c, f, i) The average (a, b, c) for all cases as well as stormy (d, e, f) and calm (g, h, i) conditions are shown where stormy exhibits Hs > 3 m and calm exhibits Hs < 0.5 m. |
|
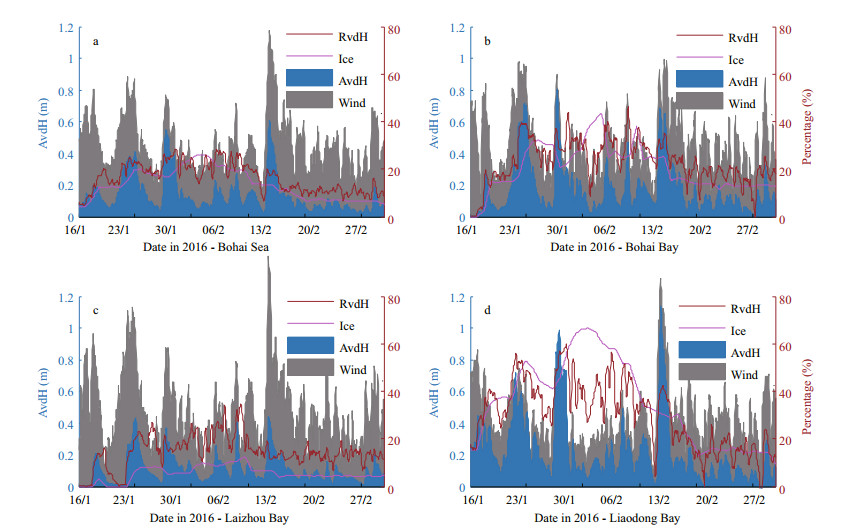
To further understand changes in simulated Hs from implementing Sice, Fig. 8 displays the time series of averaged RvdH, AvdH, wind speed and ice concentration for the Bohai Sea (Fig. 8a), Bohai Bay (Fig. 8b), Laizhou Bay (Fig. 8c) and Liaodong Bay (Fig. 8d) separately. Being consistent with Fig. 7, the biggest change in simulated Hs was from Liaodong Bay, where it reached more than 1m, and the smallest change was apparent from Laizhou Bay. Focusing on the time series, as all four subplots show, the changes in both RvdH and AvdH are highly related to wind speed variations with synchronous fluctuations. Additionally, the RvdH also correlates well with ice concentrations although it still contains the influence of wind speed as we discussed about Fig. 7. Therefore, we conclude that both stronger winds and larger ice coverage lead to greater variations in simulated Hs in the Bohai Sea.
|
| Fig.8 Average ice concentrations (solid magenta lines), RvdH (solid red lines), AvdH (blue) and wind speed (gray) for the Bohai Sea (a), Bohai Bay (b), Laizhou Bay (c) and Liaodong Bay (d) The left axis is for AvdH, the right axis is for RvdH and ice concentration. Values of wind speed are not shown, according to CFSv2, the minimum and maximum values are 1.8 m/s and 12.9 m/s, respectively. |
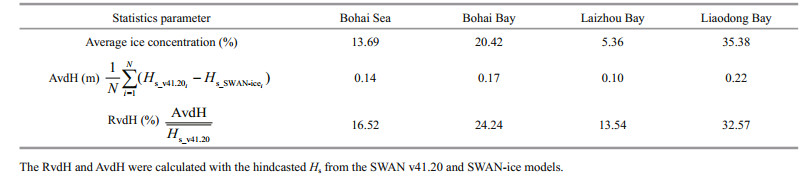
To evaluate the effect of sea ice on waves in the Bohai Sea quantitatively, the averaged AvdH and RvdH of simulated Hs between SWAN v41.20 and the SWAN-ice are listed in Table 2. Our results indicated that it might lose 16.52% accuracy of simulated Hs during the freezing period when sea ice effects on waves were ignored in the whole Bohai Sea; specifically, this rose to 32.57% in Liaodong Bay. In addition, we found that these rates approximately doubled if only the areas where sea ice may appear (ice concentration > 0) are targeted.
According to above discussions, it is found that sea ice had a significant damping effect on wave height in some areas of the Bohai Sea. But this effect had not been taken into account in previous wave climate studies (Wang et al., 2012; Lv et al., 2014), which may have led to misunderstandings of waves during the winter in the Bohai Sea. To quantify this possible deviation, we simulated Hs in the Bohai Sea from 1 January to 28 February over five years (2013–2017) with the SWAN-ice model and show the distribution of two-month averaged Hs in Fig. 9a. Then with the results of SWAN v41.20, the calculated AvdH is showed in Fig. 9b. We found that the average iceinduced wave height decrease in most of coastal regions is smaller than 0.1m, but in the Liaodong Bay, Hs is apparently overestimated by the SWAN v41.20, which ignores ice effects. During the freezing January and February, the deviation of simulated average Hs can be more than 0.3m.

|
| Fig.9 Distribution of Hs from 1 January to 28 February during 2013–2017 a. simulated averaged Hs from the SWAN-ice model; b. averaged AvdH between the SWAN v41.20 and SWAN-ice. |
In this study, we implemented an eddy viscosity wave-ice model into the SWAN v41.20 model and further apply this SWAN-ice to simulate significant wave height in the Bohai Sea for the winter with a lot of sea ice in 2016. Compared with buoy-measured wave height near the ice edge, the accuracy of hindcasts is shown to be improved from 10.42% to 1.71% by considering the ice effects on waves in the SWAN-ice. If we focus on the whole Bohai Sea, the SWAN-ice model provided 16.52% relative difference in significant wave height compared with what the SWAN v41.20 simulated. For Liaodong Bay, where sea ice is most concentrated, the absolute and relative differences reached 0.22 m and 32.57%, respectively, and these differences were enhanced during storm conditions. These results suggest that the wave damping caused by sea ice is significant during the winter in the Bohai Sea. To further evaluate the influence of sea ice on winter wave height in a climate stage, we performed a five-year (2013–2017) wave hindcast for the Bohai Sea from 1 January to 28 February each year with the SWAN-ice model. Compared with the situation regardless of sea ice, the difference of wave height was mainly concentrated in Liaodong Bay and its maximum can be more than 0.3 m.
The SWAN-ice model is not only restricted to the Bohai Sea, but can be applied to other nearshore icecovered waters as well. Compared with previous simulations that had no sea ice representation, corresponding improvements can be expected even if ice effects on wave numbers were not discussed in this study. However, currently, this type of numerical study is still limited by forcing data accuracy and model parameterizations. On the one hand, forcing winds and ice fields may miss local variations and, as a nearshore case, bathymetry resolution still has room for improvement. On the other hand, current source term functions in ice-covered water remain controversial; for example, there is no proof indicating that the eddy viscosity wave-ice model is the optimal choice for the Bohai Sea or any other nearshore waters with sea ice, nor is there unequivocal evidence for the constant parameterization of ice mechanic properties. Thus, in the future, in situ measurements are necessary to validate and calibrate wave-ice parameterizations for modeling waves that propagate through coastal ice-covered waters.
6 DADA AVAILABILITY STATEMENTThe data of the oceanographic buoys are provided by the North China Sea Marine Forecasting Center, SOA and are not publicly available. Other data used in this study are all provided in the references cited.
Amrutha M M, Kumar V S, Sandhya K G, Nair T M B, Rathod J L. 2016. Wave hindcast studies using SWAN nested in WAVEWATCH Ⅲ-comparison with measured nearshore buoy data off Karwar, eastern Arabian Sea. Ocean Engineering, 119: 114-124.
DOI:10.1016/j.oceaneng.2016.04.032 |
Battjes J A, Janssen J P F M. 1978. Energy loss and set-up due to breaking of random waves. In: Proceedings of the 16th International Conference on Coastal Engineering. ASCE, Hamburg, Germany, p.569-587.
|
Booij N, Ris R C, Holthuijsen L H. 1999. A third-generation wave model for coastal regions:1. model description and validation. Journal of Geophysical Research:Oceans, 104(C4): 7 649-7 666.
DOI:10.1029/98JC02622 |
Cheng S K, Rogers W E, Thomson J, Smith M, Doble M J, Wadhams P, Kohout A L, Lund B, Persson O P G, Collins III C O, Ackley S F, Montiel F, Shen H H. 2017. Calibrating a viscoelastic sea ice model for wave propagation in the arctic fall marginal ice zone. Journal of Geophysical Research:Oceans, 122(11): 8 770-8 793.
DOI:10.1002/2017JC013275 |
Doble M J, Bidlot J R. 2013. Wave buoy measurements at the antarctic sea ice edge compared with an enhanced ECMWF WAM:progress towards global waves-in-ice modelling. Ocean Modelling, 70: 166-173.
DOI:10.1016/j.ocemod.2013.05.012 |
Doble M J, De Carolis G, Meylan M H, Bidlot J R, Wadhams P. 2015. Relating wave attenuation to pancake ice thickness, using field measurements and model results. Geophysical Research Letters, 42(11): 4 473-4 481.
DOI:10.1002/2015GL063628 |
Eldeberky Y, Battjes J A. 1996. Spectral modeling of wave breaking:application to Boussinesq equations. Journal of Geophysical Research:Oceans, 101(C1): 1 253-1 264.
DOI:10.1029/95JC03219 |
Gemmrich J, Rogers W E, Thomson J, Lehner S. 2018. Wave evolution in off-ice wind conditions. Journal of Geophysical Research:Oceans, 123(8): 5 543-5 556.
DOI:10.1029/2018JC013793 |
Hasselmann K, Barnett T P, Bouws E, Carlson H, Cartwright D E, Enke K, Ewing J A, Gienapp H G, Hasselmann D E, Krusemann P, Meerbur A, Müller P, Olbers D J, Richter K, Sell W, Walden H. 1973. Measurements of wind-wave growth and swell decay during the joint North Sea wave project (JONSWAP). Deutches Hydrographisches Institut, Hamburg. 95p.
|
Hasselmann S, Hasselmann K, Allender J H, Barnett T P. 1985. Computations and parameterizations of the nonlinear energy transfer in a gravity-wave specturm. Part Ⅱ:parameterizations of the nonlinear energy transfer for application in wave models. Journal of Physical Oceanography, 15(11): 1 378-1 391.
DOI:10.1175/1520-0485(1985)015<1378:CAPOTN>2.0.CO;2 |
Huang B G. 2009. Numerical simulation of waves in Bohai Sea and research on the influence of swells on wind waves. Ocean University of China, Qingdao, China. 67p.(in Chinese with English abstract)
|
Khon V C, Mokhov I I, Pogarskiy F A, Babanin A, Dethloff K, Rinke A, Matthes H. 2014. Wave heights in the 21st century Arctic Ocean simulated with a regional climate model. Geophysical Research Letters, 41(8): 2 956-2 961.
DOI:10.1002/2014GL059847 |
Komen G J, Cavaleri L, Donelan M, Hasselmann K, Hasselmann S, Janssen P A E M. 1994. Dynamics and Modelling of Ocean Waves. Cambridge University Press, Cambridge, UK. 532p.
|
Komen G J, Hasselmann S, Hasselmann K. 1984. On the existence of a fully developed wind-sea spectrum. Journal of Physical Oceanography, 14(8): 1 271-1 285.
DOI:10.1175/1520-0485(1984)014<1271:OTEOAF>2.0.CO;2 |
Li J K, Kohout A L, Shen H H. 2015. Comparison of wave propagation through ice covers in calm and storm conditions. Geophysical Research Letters, 42(14): 5 935-5 941.
DOI:10.1002/2015GL064715 |
Liu A K, Holt B, Vachon P W. 1991. Wave propagation in the marginal ice zone:model predictions and comparisons with buoy and synthetic aperture radar data. Journal of Geophysical Research:Oceans, 96(C3): 4 605-4 621.
DOI:10.1029/90JC02267 |
Liu A K, Mollo-Christensen E. 1988. Wave propagation in a solid ice pack. Journal of Physical Oceanography, 18(11): 1 702-1 712.
DOI:10.1175/1520-0485(1988)018<1702:WPIASI>2.0.CO;2 |
Liu A K, Vachon P W, Peng C Y, Bhogal A S. 1992. Wave attenuation in the marginal ice zone during LIMEX. Atmosphere-Ocean, 30(2): 192-206.
DOI:10.1080/07055900.1992.9649437 |
Lv X C, Yuan D K, Ma X D, Tao J H. 2014. Wave characteristics analysis in Bohai Sea based on ECMWF wind field. Ocean Engineering, 91: 159-171.
DOI:10.1016/j.oceaneng.2014.09.010 |
Meylan M H, Bennetts L G, Kohout A L. 2014. In situ measurements and analysis of ocean waves in the Antarctic marginal ice zone. Geophysical Research Letters, 41(14): 5 046-5 051.
DOI:10.1002/2014GL060809 |
Rogers W E, Thomson J, Shen H H, Doble M J, Wadhams P, Cheng S K. 2016. Dissipation of wind waves by pancake and frazil ice in the autumn Beaufort Sea. Journal of Geophysical Research:Oceans, 121(11): 7 991-8 007.
DOI:10.1002/2016JC012251 |
Serreze M C, Stroeve J. 2015. Arctic sea ice trends, variability and implications for seasonal ice forecasting. Philosophical Transactions of the Royal Society A:Mathematical, Physical and Engineering Sciences, 373(2045): 20140159.
DOI:10.1098/rsta.2014.0159 |
Shi J, Wang P, Zhong Z, Zhang J. 2011. Comparison of ocean wave simulation with SWAN wave model using two kinds of computational grid in the Bohai Sea and the Yellow sea. Marine Forecasts, 28(4): 48-57.
(in Chinese with English abstract) |
Squire V A. 2007. Of ocean waves and sea-ice revisited. Cold Regions Science and Technology, 49(2): 110-133.
DOI:10.1016/j.coldregions.2007.04.007 |
Stroeve J C, Serreze M C, Holland M M, Kay J E, Malanik J, Barrett A P. 2012. The Arctic's rapidly shrinking sea ice cover:a research synthesis. Climatic Change, 110(3-4): 1 005-1 027.
DOI:10.1007/s10584-011-0101-1 |
Tang M N, Liu Y, LI B H, Sui J P. 2012. Analysis of the sea ice long-term trend in the bohai sea and the northern yellow sea. Marine Forecasts, 29(2): 45-49.
(in Chinese with English abstract) |
The SWAN team. 2018. Swan Scientific And Technical Documentation Swan Cycle III version 41.20AB. Delft University of Technology. http://swanmodel.sourceforge.net/. Accessed on 2019.3.28.
|
The WAMDI Group. 1988. The WAM model-a third generation ocean wave prediction model. Journal of Physical Oceanography, 18(12): 1 775-1 810.
DOI:10.1175/1520-0485(1988)018<1775:TWMTGO>2.0.CO;2 |
The WAVEWATCH-Ⅲ Development Group. 2016. User manual and system documentation of WAVEWATCH Ⅲ version 5.16. Tech. Note 329, NOAA/NWS/NCEP/MMAB, College Park, MD, USA, 326 pp.+ Appendices. https://polar.ncep.noaa.gov/waves/wavewatch/. Accessed on 2019.3.28.
|
Thomson J, Ackley S, Girard-Ardhuin F, Ardhuin F, Babanin A, Boutin G, Brozena J, Cheng S K, Collins C, Doble M, Fairall C, Guest P, Gebhardt C, Gemmrich J, Graber H C, Holt B, Lehner S, Lund B, Meylan M H, Maksym T, Montiel F, Perrie W, Persson O, Rainville L, Rogers W E, Shen H, Shen H, Squire V, Stammerjohn S, Stopa J, Smith M M, Sutherland P, Wadhams P. 2018. Overview of the arctic sea state and boundary layer physics program. Journal of Geophysical Research:Oceans, 123(12): 8 674-8 687.
DOI:10.1002/2018jc013766 |
Thomson J, Rogers W E. 2014. Swell and sea in the emerging Arctic Ocean. Geophysical Research Letters, 41(9): 3 136-3 140.
DOI:10.1002/2014GL059983 |
Tolman H L. 1991. A third-generation model for wind waves on slowly varying, unsteady, and inhomogeneous depths and currents. Journal of Physical Oceanography, 21(6): 782-797.
DOI:10.1175/1520-0485(1991)021<0782:ATGMFW>2.0.CO;2 |
Wadhams P, Squire V A, Goodman D J, Cowan A M, Moore S C. 1988. The attenuation rates of ocean waves in the marginal ice zone. Journal of Geophysical Research:Oceans, 93(C6): 6 799-6 818.
DOI:10.1029/JC093iC06p06799 |
Wang R X, Shen H H. 2010. Gravity waves propagating into an ice-covered ocean:a viscoelastic model. Journal of Geophysical Research:Oceans, 115(C6): C06024.
DOI:10.1029/2009JC005591 |
Wang Z F, Dong S, Li X, Soares C G. 2016. Assessments of wave energy in the Bohai Sea, China. Renewable Energy, 90: 145-156.
DOI:10.1016/j.renene.2015.12.060 |
Wang Z F, Wu K J, Zhou L M, Wu L Y. 2012. Wave characteristics and extreme parameters in the Bohai Sea. China Ocean Engineering, 26(2): 341-350.
DOI:10.1007/s13344-012-0026-0 |
Yin B S, Yang D Z, Sha R N, Cheng M H. 2005. Improvement of different source function expressions in SWAN model for the Bohai Sea. Progress in Natural Science, 15(8): 720-724.
DOI:10.1080/10020070512331342820 |
Zhang Y J, Jin B F, Feng X. 2007. Response of the sea ice conditions in the Bohai Sea to global climate change in the last over half century. Marine Science Bulletin, 26(6): 96-101.
(in Chinese with English abstract) |
Zhao X, Shen H H, Cheng S K. 2015. Modeling ocean wave propagation under sea ice covers. Acta Mechanica Sinica, 31(1): 1-15.
DOI:10.1007/s10409-015-0017-5 |
 2019, Vol. 37
2019, Vol. 37


