Institute of Oceanology, Chinese Academy of Sciences
Article Information
- LIU Qian, SHANG Xiaodong, XIE Xiaohui
- Observations of semidiurnal M2 internal tidal parametric subharmonic instability in the northeastern South China Sea
- Journal of Oceanology and Limnology, 39(1): 56-63
- http://dx.doi.org/10.1007/s00343-019-9131-8
Article History
- Received May. 20, 2019
- accepted in principle Sep. 19, 2019
- accepted for publication Dec. 16, 2019
2 State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, China;
3 Southern Marine Science and Engineering Guangdong Laboratory, Guangzhou 511458, China;
4 State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Ministry of Natural Resources, Hangzhou 310000, China
Resonant interactions among internal waves are regarded as one of processes being responsible for energy transfer in the ocean internal wave spectrum (McComas and Bretherton, 1977). In general, they appear in the form of triads in the fluid dynamics. For ocean linear (free) internal waves with wavenumbers ki and frequencies ωi (i=1, 2, 3, etc.), the dispersion relation is:
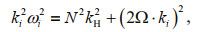 (1)
(1)where kH is horizontal wavenumber, N is the buoyancy frequency, and Ω is the Earth's rotation vector. If there are three free waves in internal wave spectrum and their wavenumbers and frequencies satisfy the following resonant condition:
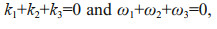 (2)
(2)Energy will be systematically transferred amongst three waves (Müller et al., 1986). Parametric subharmonic instability (PSI), which transfers energy from an energetic parent wave with frequency ω and low vertical wavenumber kz to two daughter waves with frequency near ω/2 and higher kz, is one of the above nonlinear resonant interactions. Since shear instabilities induced by motions with high kz can generate breaking internal waves that are the major source of deep-sea mixing (Munk and Wunsch, 1998), the PSI process has received considerable attention in the past 10 years.
Most of previous numerical models investigated PSI of internal tides (internal waves with tidal frequency), especially for semidiurnal M2 (12.42 h period) internal tides (Hibiya et al., 2002; MacKinnon and Winters, 2005; Gerkema et al., 2006; Korobov and Lamb, 2008; Simmons, 2008). Since frequencies of ocean free internal gravity waves are greater than the local inertial frequency f=2Ωsinφ, twice the local vertical component of Ω at latitude φ, the PSI process of semidiurnal internal tides ocean only occurs at latitudes equatorward of the diurnal "critical latitude" φd (~29°), where 0.5M2=f, unless the internal wave band is broadened or the instability is no longer a resonant triad interaction (Korobov and Lamb, 2008; Xie et al., 2016). These model results also indicated that the process is most efficient at φd because energy of M2 is here transferred to approximately pure inertial waves (i.e., 0.5M2=f).
Open ocean observations from field experiments (Hibiya and Nagasawa, 2004; van Haren, 2005; Kunze et al., 2006; Alford et al., 2007) confirmed the occurrence of semidiurnal internal tidal PSI and suggested that the PSI process may play an important role in the cascade of low mode internal tidal energy down to small dissipation scales available for mixing. Compared with the open ocean, the South China Sea (SCS), which is located between the equator and 25°N and is one of the largest marginal seas of the Pacific, features stronger diurnal O1 (25.82 h period) and K1 (23.93 h period) internal tidal waves with respect to M2. As a result, PSI from diurnal internal tides is also found near the bi-diurnal critical latitude (~14°), where f is equal to half of diurnal frequency (Alford et al., 2007; Simmons, 2008; Xie et al., 2009, 2016). Since the PSI course of the semidiurnal M2 internal tides is most efficient at φd, previous observational studies for PSI of internal tides mostly focused on the area near φd. However, due to 0.5M2≈f at φd, subharmonic motions are easily contaminated by wind-induced near-inertial waves with a broad frequency band so that their physical features are difficult to be distinguished. Hence, the survey for internal tidal PSI away from φd is necessary.
The cruise observations of Carter and Gregg (2006) have shown a rapid energy transfer from M2 to 0.5M2 in close proximity to the internal tide generation region at low latitudes away from φd. In the SCS away from φd, Xie et al.(2008, 2011, 2013) indicated the occurrence of PSI of semidiurnal internal tides. However, some important physical properties of daughter waves within a PSI triad are still unclear although they have been definitely predicted in classical PSI theory. In this paper, one set of 75-d long ADCP (acoustic Doppler current profile) record collected in the northeastern SCS is used to investigate the PSI course of the semidiurnal M2 internal tide away from φd. The major purpose is to make physical characteristics of daughter waves in a PSI triad become clear and suggest that PSI may be an important mechanism that cascade low-mode internal tidal energy down to small dissipation scales in the South China Sea away from φd. In addition, we also suggest a new method that can be used to identify the occurrence of internal tidal PSI.
2 DATA AND METHOD 2.1 DataOcean current data were collected at a mooring site (118.41°E, 20.58°N) in the South China Sea, where the water depth is 2 474 m (Fig. 1). The mooring was equipped with an upward-looking WHL75-I-Z ADCP deployed at ~450 m (data from 436 to 52 m, 16-m bins) and five Aanderra current meters at depths of 800, 1 000, 1 500, 2 000, and 2 300 m. The mooring time was from August 2000 to March 2001. Unfortunately, the ADCP worked only for the first ~75 d (from August 20 to November 4, 2000) and current meters at depths of 800 and 1 000 m were broken due to some incorrect settings before deployment. Another current meter at depth of 1 500 m worked only for the first ~20 d, which was not used in this study. The samplings of the ADCP and current meters were 15 and 30 min, respectively.
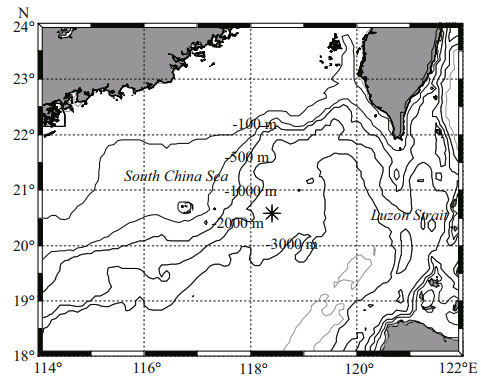
|
| Fig.1 Bathymetry of the South China Sea and mooring location (the asterisk) |
Using a second-order Butterworth filter, the current velocities ([u, v]) and first-difference velocity shear ([∂u/∂z, ∂v/∂z]) at all observed depths are band-pass filtered to extract diurnal (D1) and semidiurnal (D2) components. Hereafter, we use Di (i=1, 2, 3, etc.) to represent an (over-) harmonic diurnal band if no specific harmonic frequency is indicated. The filter bounds of D1 and D2 are [0.9 O1, 1.1 K1] and [0.9, 1.1] M2, respectively.
Since our observation site was located in the deepsea basin near the Luzon Strait (LS) (~210 km from the LS), where strong internal tides and much weaker barotropic tides exist (Lien et al., 2005; Zu et al., 2008), the barotropic and baroclinic signals are not separated. The effects of barotropic tides are negligible.
2.3 Rotary spectral estimationLet the east-west (u) and north-south (v) currents (or the first-difference velocity shears [∂u/∂z, ∂v/∂z]) observed by the ADCP in a horizontal plane be combined into one complex variable
 (3)
(3)and its Fourier series can be written as
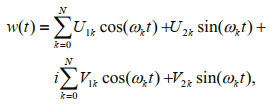 (4)
(4)where i2=-1, ωk=2πσk=2πk/T (T is the record length) is the angular frequency, and (Uk, Vk) are the amplitudes. Since any horizontal current ellipse is a sum of clockwise (-) and anticlockwise (+) components (Gonella, 1972), the time series of the kth frequency component becomes
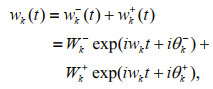 (5)
(5)where Wk and θk represent amplitude and phase angle, respectively. The clockwise and anticlockwise rotary component amplitudes can be calculated by:
 (6a)
(6a)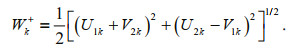 (6b)
(6b)Define total rotary amplitude spectra as:
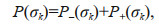 (7)
(7)where P-(σk) is the clockwise rotary spectrum:
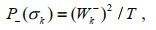 (8a)
(8a)and P+(σk) is the anticlockwise rotary spectrum:
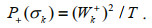 (8b)
(8b)The total amplitude spectrum computed from velocity (shear) is also called as the kinetic energy (shear) spectrum.
Since there are different spectral features between clockwise and anticlockwise components, they can be utilized to measure the polarization of internal gravity waves, for which Gonella (1972) introduced the "rotary coefficient"
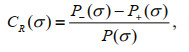 (9)
(9)where CR is equal to zero and one for purely rectilinear and purely circular motions, respectively. Under linear perturbation and neglecting frictional stress, the Eq.9 becomes (Gonella, 1972; van Haren, 2003),
 (10)
(10)Within the internal wave band (f < σ < N), the solution of Eq.10 describes free internal gravity waves. According to PSI theory (Eqs.1 & 2), three waves within a PSI triad should be free waves; that is, their CR values should be consistent with Eq.10. Thus, the rotary spectral method can provide a possibility to identify PSI.
3 OBSERVATION 3.1 Tidal currentsFigure 2 presents a time-depth map of band-pass filtering meridional velocity the D1 and D2 velocity amplitudes Ud and Usd(U=(u, v)) (Fig. 2a & b), where the signals with semidiurnal and diurnal periods are evidently visible. The largest velocity amplitudes for both tidal motions are often found in upper depth bins, indicating the strong prevalence of internal tides over the barotropic.

|
| Fig.2 Time-depth maps of diurnal (a) and semidiurnal (b) velocity amplitude |
In the meantime, the heightened Ud and Usd shows a clear, fortnightly spring-neap cycle. D1 and D2 have strikingly different spatial and temporal structures(Fig. 2a & b). In depth, D1 show considerable variations relative to D2 that display the dominance of relatively large-scale vertical motions. The diurnal 14-d cycle becomes vague under 200 m (Fig. 2a). In time, phase of the diurnal and semidiurnal 14-cycle is nearly opposite. However, a relatively weak aggrandizement of Ud during September 3–8 below depth of 164 m occurs at the (second) semidiurnal spring tide, rather than at diurnal. The observed maximum velocity amplitude is up to 0.25 m/s.
As a result, the significant spectral peaks are observed in diurnal frequency band D1 and semidiurnal frequency band D2 (Fig. 3). In kinetic energy spectra, the inertial peak (f) is also outstanding, clearly distinguished from D1. In addition to these fundamental inertial and tidal frequency bands, large energy is also observed at some higher tidal harmonic bands (e.g., D3, D4, …), suggesting strong nonlinear couplings between internal tidal waves (Xie et al., 2011).

|
| Fig.3 Kinetic energy spectra (v≈3 degrees of freedom; dof) at depths of 68 m (black line), 228 m (gray line) and 388 m (dashed line) |
The maximum harmonics in D1 show obvious variation in depth. In the shallow water (i.e., 68 m), D1 is dominated by O1 and K1 constituents with comparable spectral amplitude (Fig. 3). As depth increases, energy at both O1 and K1 weakens but the reduction at K1 is much larger than that at O1. At depth of 338 m, a non-tidal harmonic 0.5 M2 becomes dominant in D1, implying that PSI of the M2 internal tides may occur at the mooring site and energy is transferred from the M2 internal tides to the subharmonic 0.5 M2 (McComas and Bretherton, 1977). In D2, M2, and S2 are dominant, and their spectral amplitude is reduced with increasing depth.
The dominant O1 and K1 harmonics in D1 appear in the upper 200 m only, where the diurnal 14-d springneap cycle induced by their interference was clearly observed (Fig. 2a). In D2, kinetic energy spectra at all depth bins show that semidiurnal tidal components M2 and S2 are dominant (Fig. 3). Their interference creates a semidiurnal 14-d spring-neap cycle (Fig. 2b). The phase of the semidiurnal 14-d cycle is almost opposite to that of diurnal tides. Below 200 m, the diurnal 14-d cycle becomes ambiguous due to weakened O1 and K1. The elevated diurnal velocity amplitude Ud is also observed at semidiurnal springs (Fig. 2a). This may be because 0.5 M2 have energy comparable to O1 and K1 in the lower layer (Fig. 3), which further suggests that 0.5 M2 may result from PSI of the semidiurnal internal tides.
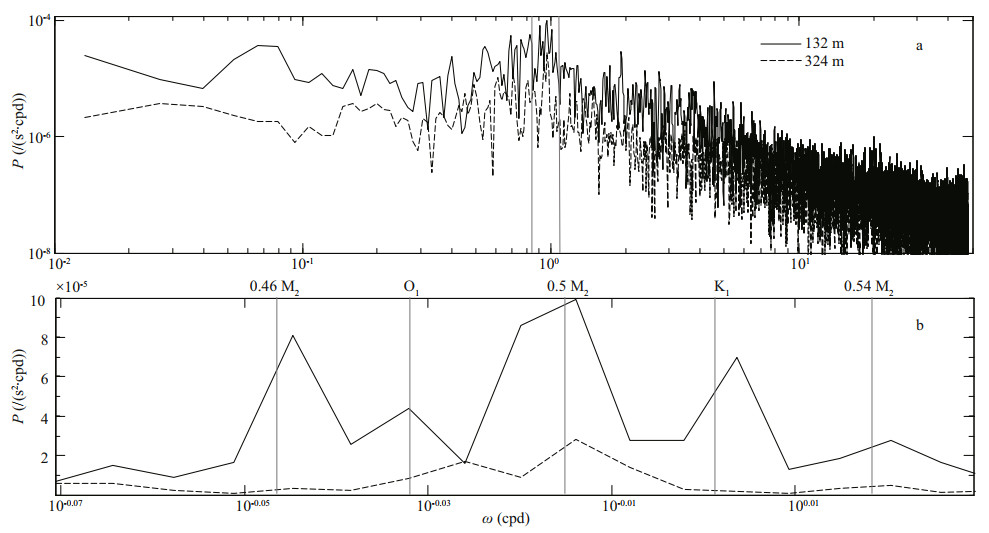
3.2 Diurnal velocity shearFigure 4a shows the first-difference shear spectrum at depths of 132 m and 324 m. The largest shear appears in D1. Although D2 has strong signal in velocity, it is weak in shear, indicating that the semidiurnal energy is borne primarily by low-mode. To identify which harmonics dominate over D1, the diurnal band is given in Fig. 4b. At two depths (132 m and 324 m), the largest peak appeared at 0.5 M2. At depth of 132 m, the peaks are also found at 0.46 M2, O1, K1, and 0.54 M2, while D1 is dominated by 0.5 M2 at depth of 324 m (Fig. 4b).
|
| Fig.4 Shear spectra (v≈3 degrees of freedom; dof)) at depths of 132 m (black line) and 324 m (dashed line) (a) and the diurnal band (b) as shown by the two gray lines |
Figure 5 shows time series of diurnal and semidiurnal velocity averaged over depths above 180 m. Comparing with Ud, it is found that diurnal velocity shears show some different variations (Fig. 5b). The diurnal 14-d cycle is inconspicuous in the shear field. Large Ud during diurnal spring tide does not noticeably elevate shear, suggesting the dominance of low-mode diurnal internal tidal waves (Fig. 5a & b). In contrast, the enlarged diurnal shear amplitude Sd (S=(Su, Sv)) often appears at diurnal (semidiurnal) neap (spring) tide (Fig. 5c). Such observation is especially evident near 324-m depth, where the heightened Sd for the entire observation period closely follows the semidiurnal spring-neap cycle by lags of a few (1–3) d (Fig. 5b). This strongly suggests that energy of diurnal waves elevating Sd during semidiurnal springs is mainly supplied by semidiurnal tides. At depth of 132 m, where the largest peak not only appears at O1 and K1 but also happens at nonlinear coupling frequencies 0.46 M2, 0.54 M2 and 0.5 M2, the elevated Sd is observed at both diurnal and semidiurnal spring tides. The harmonics 0.46 M2, 0.54 M2 and M2 may also consist of another triad. These observations suggest that energy of high-mode diurnal waves elevating Sd during semidiurnal springs is mainly supplied by semidiurnal tides.

|
| Fig.5 Time series of diurnal (blue) and semidiurnal (red) velocity averaged over depths above 180 m (a); time-depth map of diurnal vertical shear amplitude (b); time series of diurnal shear amplitude at depths of 132 m and 324 m (c) |
Figure 6 shows the time-depth maps of meridional diurnal shear during five diurnal spring tides and five semidiurnal spring tides. Since the first-difference shear removes barotropic signals and most of lowmode baroclinic signals, the depth-time maps of meridional velocity shears clearly show the diurnal internal waves with high vertical wavenumbers (kz) during the five semidiurnal springs in the entire observational period (Fig. 6b). These suggest that the enlarged diurnal shear during semidiurnal springs is mainly supplied by semidiurnal tides. Furthermore, the vertically-standing signals are clearly visible in these periods, suggesting the superposition of the upward and downward propagating subharmonics (0.5 M2). The checkerboard pattern that is often observed when PSI occurs (Carter and Gregg, 2006; Alford et al., 2007; Xie et al., 2016) can also be clearly identified at the last two semidiurnal springs. Notably the time-depth maps of diurnal shear between about 130 m and 280 m depth at the last two semidiurnal springs show clearly checkerboard pattern. On the contrast, the diurnal shear signals during diurnal springs show relatively low kz and the verticallystanding signals become ambiguous (Fig. 6a). These observations further confirm that diurnal subharmonics 0.5 M2 observed during semidiurnal springs are generated by PSI of the semidiurnal internal tides.

|
| Fig.6 Time-depth maps of diurnal shear in v during five diurnal spring tides (a) and five semidiurnal spring tides (b) |
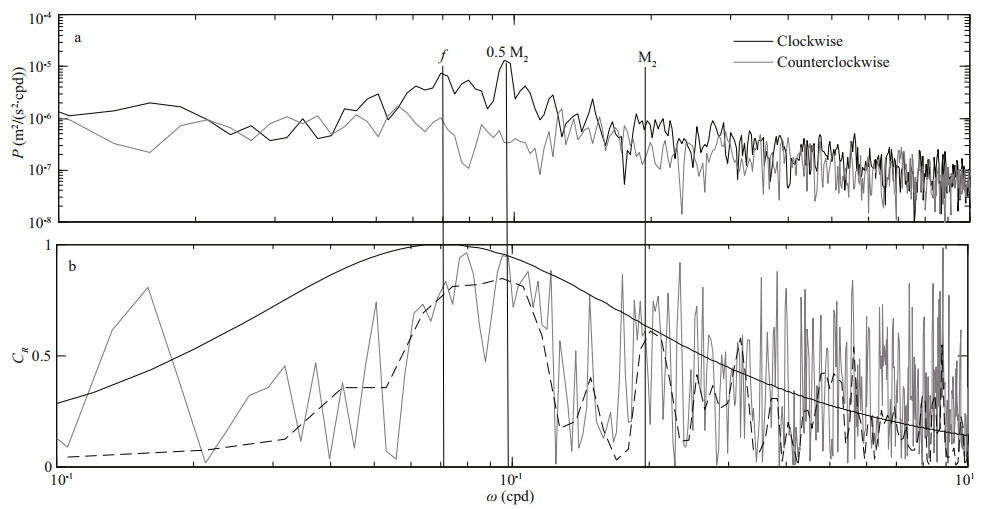
Since semidiurnal subharmonic waves can be dominant in the shear field for the entire observation record, we examine their rotary coefficients (CR) via rotary shear spectra. Under the WKB approximation, internal gravity wave' polarizations are not changed by vertical shear (∂(u, v)/∂z). Therefore, CR computed by rotary shear spectra can still reveal the same internal wave' polarization with those calculated by rotary velocity spectra. Figure 7a shows shear spectra with two rotary components and CR spectra computed by them around the depth of 324 m, where D1 is dominated by 0.5 M2 and there is a remarkable persistent energy exchange from semidiurnal internal tides to their subharmonic waves in the entire observation period (Fig. 5b). In the low-frequency internal wave band, the clockwise component dominates over the counterclockwise component (Fig. 7a). As a result, the largest CR value was found at these frequencies whether in weakly or moderately smoothed CR spectra (Fig. 7b). At 0.5 M2 frequency, the observed CR value (=0.947) is closely equal to what is expected for a free 0.5 M2 wave estimated in Eq.10 (Fig. 7b).
|
| Fig.7 Clockwise (black line) and counterclockwise (gray line) rotary spectra at depth of 324 m (5 dofs) (a); CR spectra (gray line: 5 dofs; dashed line: 26 dofs) at depth of 324 m (b) The black curve is the result of Eq.10. |
We have clearly presented PSI-observations of semidiurnal M2 internal tides away from the "critical" latitude for 0.5 M2 (28.8°N) from a set of 75-d long ADCP data obtained at the SCS. In addition to provide several observational proofs for identifying PSI, the fast energy transfer between daughter and parent waves within two crossed internal tidal beams was revealed. The diurnal velocity and shear fields dominated by subharmonic waves can be often characterized with nearly vertically-standing signals due to the superposition of two daughters with nearly opposite (high) vertical wavenumbers and nearly equal frequencies in a PSI-triad. The semidiurnal M2 internal tide within the observed triads cannot only transfer its energy to near-diurnal waves with perfectly half its frequency, but also those with approximately half its frequency. Besides, subharmonic waves had a rotary spectral property that was consistent with what was previously called "linear wave" theory and which may imply that they are subjected to an approximate linear dispersion relation σi=Ω(ki), as expected from PSI theory. Rotary spectra provide a new evidence for observations of PSI mechanism in the ocean. Furthermore, subharmonic waves occurred in burst following the semidiurnal spring tide by lags of a few (1–3) d, suggesting a fast energy transfer from semidiurnal internal tides to their daughter waves.
5 DATA AVAILABILITY STATEMENTThe data that support the findings of this study are available from the corresponding author upon reasonable request.
Alford M H, MacKinnon J A, Zhao Z X, Pinkel R, Klymak J, Peacock T. 2007. Internal waves across the Pacific. Geophysical Research Letters, 34(24): L24601.
DOI:10.1029/2007GL031566 |
Carter G S, Gregg M C. 2006. Persistent near-diurnal internal waves observed above a site of M2 barotropic-to-baroclinic conversion. Journal of Physical Oceanography, 36(6): 1 136-1 147.
DOI:10.1175/JPO2884.1 |
Gerkema T, Staquet C, Bouruet-Aubertot P. 2006. Decay of semi-diurnal internal-tide beams due to subharmonic resonance. Geophysical Research Letters, 33(8): L08604.
|
Gonella J. 1972. A rotary-component method for analysing meteorological and oceanographic vector time series. Deep Sea Research and Oceanographic Abstracts, 19(12): 833-846.
DOI:10.1016/0011-7471(72)90002-2 |
Hibiya T, Nagasawa M, Niwa Y. 2002. Nonlinear energy transfer within the oceanic internal wave spectrum at mid and high latitudes. Journal of Geophysical Research, 107(C11): 3207.
DOI:10.1029/2001JC001210 |
Hibiya T, Nagasawa M. 2004. Latitudinal dependence of diapycnal diffusivity in the thermocline estimated using a finescale parameterization. Geophysical Research Letters, 31(1): L01301.
|
Korobov A S, Lamb K G. 2008. Interharmonics in internal gravity waves generated by tide-topography interaction. Journal of Fluid Mechanics, 611: 61-95.
DOI:10.1017/S0022112008002449 |
Kunze E, Firing E, Hummon J M, Chereskin T K, Thurnherr A M. 2006. Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles. Journal of Physical Oceanography, 36(8): 1 553-1 576.
DOI:10.1175/JPO2926.1 |
Lien R C, Tang T Y, Chang M H, D'Asaro E A. 2005. Energy of nonlinear internal waves in the South China Sea. Geophysical Research Letters, 32(5): L05615.
|
MacKinnon J A, Winters K B. 2005. Subtropical catastrophe:significant loss of low-mode tidal energy at 28.9°. Geophysical Research Letters, 32(15): L15605.
DOI:10.1029/2005GL023376 |
Mccomas C H, Bretherton F P. 1977. Resonant interaction of oceanic internal waves. Journal of Geophysical Research, 82(9): 1 397-1 412.
DOI:10.1029/JC082i009p01397 |
Müller P, Holloway G, Henyey F, Pomphrey N. 1986. Nonlinear interactions among internal gravity waves. Reviews of Geophysics, 24(3): 493-536.
DOI:10.1029/RG024i003p00493 |
Munk W, Wunsch C. 1998. Abyssal recipes Ⅱ:energetics of tidal and wind mixing. Deep Sea Research Part I:Oceanographic Research Papers, 45(12): 1 977-2 010.
DOI:10.1016/S0967-0637(98)00070-3 |
Simmons H L. 2008. Spectral modification and geographic redistribution of the semi-diurnal internal tide. Ocean Modelling, 21(3-4): 126-138.
DOI:10.1016/j.ocemod.2008.01.002 |
van Haren H. 2003. On the polarization of oscillatory currents in the Bay of Biscay. Journal of Geophysical Research, 108(C9): 3290.
DOI:10.1029/2002JC001736 |
van Haren H. 2005. Tidal and near-inertial peak variations around the diurnal critical latitude. Geophysical Research Letters, 32(23): L23611.
DOI:10.1029/2005GL024160 |
Xie X H, Chen G Y, Shang X D, Fang W D. 2008. Evolution of the semidiurnal (M2) internal tide on the continental slope of the northern South China Sea. Geophysical Research Letters, 35(13): L13604.
DOI:10.1029/2008GL034179 |
Xie X H, Liu Q, Shang X D, Chen G Y, Wang D X. 2016. Poleward propagation of parametric subharmonic instability-induced inertial waves. Journal of Geophysical Research, 121(3): 1 881-1 895.
|
Xie X H, Shang X D, Chen G Y, Sun L. 2009. Variations of diurnal and inertial spectral peaks near the bi-diurnal critical latitude. Geophysical Research Letters, 36(2): L02606.
|
Xie X H, Shang X D, van Haren H, Chen G Y, Zhang Y Z. 2011. Observations of parametric subharmonic instability-induced near-inertial waves equatorward of the critical diurnal latitude. Geophysical Research Letters, 38(5): L05603.
|
Xie X H, Shang X D, van Haren H, Chen G Y. 2013. Observations of enhanced nonlinear instability in the surface reflection of internal tides. Geophysical Research Letters, 40(8): 1 580-1 586.
DOI:10.1002/grl.50322 |
Zu T T, Gan J P, Erofeeva S Y. 2008. Numerical study of the tide and tidal dynamics in the South China Sea. Deep Sea Research Part I:Oceanographic Research Papers, 55(2): 137-154.
DOI:10.1016/j.dsr.2007.10.007 |
 2021, Vol. 39
2021, Vol. 39


